Il trapezio
Il trapezio è un poligono avente quattro lati, di cui almeno un paio sono paralleli, denominati basi. La distanza tra le basi è chiamata altezza. I lati non paralleli sono detti gambe o lati obliqui. Un trapezio può essere classificato in diverse categorie, basandosi sulle caratteristiche dei suoi lati e angoli:
- Trapezio rettangolo: un trapezio con un angolo retto.
- Trapezio isoscele: un trapezio in cui le gambe sono congruenti, ovvero hanno la stessa misura.
- Trapezio scaleno: un trapezio senza lati uguali o angoli eguali.
I trapezi possono essere ulteriormente distinti in base all’orientamento delle basi:
- Trapezio ordinario: le basi sono su due linee parallele.
- Trapezio irregolare: le basi non sono su linee parallele.
Le proprietà principali del trapezio includono:
- Somma degli angoli interni: equivarà a 360°, come per qualsiasi quadrilatero.
- Linea media: un segmento che collega i punti medi delle gambe, la cui lunghezza è la media aritmetica delle lunghezze delle due basi.
Esempio di trapezio isoscele
| Proprietà | Descrizione |
|---|---|
| Basi parallele | Due, di lunghezza differente |
| Gambe | Uguali in lunghezza |
| Angoli alla base | Uguali tra loro |
| Altezza | Perpendicolare alle basi e uguale per entrambe |
Il perimetro di un trapezio è dato dalla somma delle lunghezze di tutti i lati. Per la sua misurazione si utilizza una formula specifica che tiene conto delle lunghezze delle basi e delle gambe.
Calcolare il perimetro del trapezio
Il perimetro di un trapezio è la somma delle lunghezze dei suoi quattro lati. La formula specifica varia a seconda del tipo di trapezio: isoscele, rettangolo o scaleno.
Perimetro Trapezio Isoscele
Perimetro Trapezio Rettangolo
Perimetro Trapezio Scaleno
Perimetro di un trapezio isoscele
Un trapezio isoscele ha due lati non paralleli di uguale lunghezza. Il perimetro ( P ) è dato dalla formula:
![]()
dove ![]() e
e ![]() sono le basi e
sono le basi e ![]() è la lunghezza dei lati obliqui.
è la lunghezza dei lati obliqui.
Perimetro di un trapezio rettangolo
In un trapezio rettangolo, uno dei lati non paralleli è perpendicolare alle basi. Per calcolare il perimetro ( P ), si utilizza la formula:
![]()
qui, ![]() e
e ![]() rappresentano le basi mentre
rappresentano le basi mentre ![]() e
e ![]() sono i lati, con
sono i lati, con ![]() perpendicolare alle basi.
perpendicolare alle basi.
Perimetro di un trapezio scaleno
Il trapezio scaleno non ha lati uguali né angoli uguali. Il perimetro si ottiene sommando tutte e quattro le lunghezze dei lati:
![]()
Dove ![]() e
e ![]() sono le due basi e
sono le due basi e ![]() ,
, ![]() i lati obliqui.
i lati obliqui.
Formule generali per il perimetro
Il perimetro di un trapezio può essere calcolato sommando la lunghezza di tutti i suoi lati. Un trapezio è un quadrilatero con almeno un paio di lati paralleli, denominati base maggiore ![]() e base minore
e base minore ![]() , mentre i lati non paralleli sono chiamati lati obliqui
, mentre i lati non paralleli sono chiamati lati obliqui ![]() e
e ![]() . La formula generale per il perimetro P di un trapezio è quindi data da:
. La formula generale per il perimetro P di un trapezio è quindi data da:![]()
Di seguito è riportata una tabella che riassume le componenti utilizzate nella formula del perimetro del trapezio:
| Componente | Descrizione |
|---|---|
| Lunghezza della base maggiore | |
| Lunghezza della base minore | |
| Lunghezza del primo lato obliquo | |
| Lunghezza del secondo lato obliquo |
Per determinare il perimetro, ogni lunghezza deve essere misurata con precisione. In alcuni casi, quando non è immediato dedurre la misura dei lati obliqui, si possono applicare teoremi geometrici o formule trigonometriche all’interno del trapezio, per calcolarli indirettamente partendo dalle misure disponibili e dalle proprietà del trapezio.
Qui di seguito un esempio di come applicare la formula:
Siano ![]() = 10 cm,
= 10 cm, ![]() = 6 cm,
= 6 cm, ![]() = 5 cm, e
= 5 cm, e ![]() = 7 cm, il perimetro sarà:
= 7 cm, il perimetro sarà:![]() = 10 cm + 6 cm + 5 cm + 7 cm = 28 cm
= 10 cm + 6 cm + 5 cm + 7 cm = 28 cm
La misura precisa dipende dall’accuratezza delle lunghezze date per ogni componente del trapezio.
Esempi di calcolo del perimetro
Il perimetro di un trapezio si calcola sommando la lunghezza dei suoi quattro lati. Si indica con la formula ![]() , dove
, dove ![]() e
e ![]() sono le basi e
sono le basi e ![]() e
e ![]() i lati obliqui. Di seguito si illustrano due esempi pratici di calcolo del perimetro di un trapezio.
i lati obliqui. Di seguito si illustrano due esempi pratici di calcolo del perimetro di un trapezio.
Esempio 1:
Un trapezio isoscele con base maggiore ![]() di 10 cm, base minore
di 10 cm, base minore ![]() di 6 cm e i lati obliqui
di 6 cm e i lati obliqui ![]() e
e ![]() lunghi 5 cm ciascuno.
lunghi 5 cm ciascuno.
| Base Maggiore [/latex] b_1 [/latex] | Base Minore | Lato Obliquo | Lato Obliquo |
|---|---|---|---|
| 10 cm | 6 cm | 5 cm | 5 cm |
Calcolo del perimetro: ![]() = 10 cm + 6 cm + 5 cm + 5 cm = 26 cm
= 10 cm + 6 cm + 5 cm + 5 cm = 26 cm
Esempio 2:
Un trapezio rettangolare con base maggiore ![]() di 12 cm, base minore
di 12 cm, base minore ![]() di 7 cm, altezza
di 7 cm, altezza ![]() di 5 cm e un lato obliquo (
di 5 cm e un lato obliquo (![]() che si calcolerà mediante il teorema di Pitagora applicato al triangolo rettangolo formato dall’altezza e dalle due basi.
che si calcolerà mediante il teorema di Pitagora applicato al triangolo rettangolo formato dall’altezza e dalle due basi.
| Base Maggiore | Base Minore | Altezza | Lato Obliquo |
|---|---|---|---|
| 12 cm | 7 cm | 5 cm | √[(5 cm)² + (5 cm)²] |
Lunghezza del lato obliquo: ![]() = √(25 cm² + 25 cm²) = √50 cm² = 7.07 cm (approssimato a due decimali)
= √(25 cm² + 25 cm²) = √50 cm² = 7.07 cm (approssimato a due decimali)
Calcolo del perimetro: ![]() = 12 cm + 7 cm + 5 cm + 7.07 cm = 31.07 cm
= 12 cm + 7 cm + 5 cm + 7.07 cm = 31.07 cm
Questi esempi evidenziano come la geometria e l’aritmetica di base consentono di determinare il perimetro di trapezi con diverse forme e proporzioni.
Misurazione dei lati del trapezio
Per calcolare il perimetro di un trapezio è essenziale misurare con precisione i quattro lati. Il trapezio è un quadrilatero con due lati paralleli di lunghezze diverse, denominati base maggiore ![]() e base minore
e base minore ![]() , e due lati non paralleli, chiamati lati obliqui [/latex] l_1 [/latex] e
, e due lati non paralleli, chiamati lati obliqui [/latex] l_1 [/latex] e ![]() .
.
Procedura di Misurazione:
- Posizionare il trapezio su una superficie piana.
- Utilizzare un metro a nastro o un righello per misurare la base maggiore
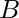 , la base minore
, la base minore 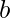 , e i lati obliqui
, e i lati obliqui 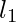 e
e 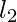 . Assicurarsi che lo strumento di misura sia allineato correttamente al lato per una lettura accurata.
. Assicurarsi che lo strumento di misura sia allineato correttamente al lato per una lettura accurata.
Tabella delle misure:
| Lato | Strumento di Misura | Lunghezza (cm) |
|---|---|---|
| Base maggiore | Metro a nastro | da definire |
| Base minore | Metro a nastro | da definire |
| Lato obliquo | Righello o metro | da definire |
| Lato obliquo | Righello o metro | da definire |
Suggerimenti Utili:
- Verificare che lo strumento di misura sia a contatto con il lato lungo tutto il suo sviluppo.
- Misure ripetute aumentano l’accuratezza.
- Alle volte, può essere utile utilizzare un angolo retto per assicurarsi dell’allineamento corretto dello strumento di misura con i lati obliqui del trapezio.
Una volta registrate le lunghezze, sommare i valori dei quattro lati per ottenere il perimetro del trapezio. La formula del perimetro è data dalla somma delle lunghezze dei lati: ![]() =
= ![]() +
+ ![]() +
+ ![]() +
+ ![]() .
.
Strumenti di calcolo online
Gli strumenti di calcolo online sono applicazioni web che permettono agli utenti di calcolare il perimetro di un trapezio inserendo i valori delle lunghezze dei lati. Questi strumenti sono progettati per fornire risultati rapidi e accurati, evitando calcoli manuali complessi.
Caratteristiche principali:
- Facilità d’uso: Interfaccia utente intuitiva.
- Accessibilità: Disponibili su vari dispositivi connessi a internet.
- Efficienza: Riduzione dell’errore umano nei calcoli.
| Vantaggi | Descrizione |
|---|---|
| Risparmio di tempo | Il calcolo è istantaneo dopo l’immissione dei dati. |
| Nessun costo | Solitamente disponibili gratuitamente. |
| Aggiornamenti continui | Costanti miglioramenti delle funzionalità e dell’interfaccia. |
Gli strumenti offrono, inoltre, istruzioni per il calcolo manuale e spesso includono formule e definizioni ai fini educativi. Questi strumenti possono essere di grande aiuto sia per studenti che per professionisti che necessitano di calcolare il perimetro trapezoidale in contesti geometrici o applicativi.
Applicazioni pratiche del perimetro del trapezio
Il perimetro del trapezio è una misura fondamentale in diverse discipline e applicazioni pratiche. In architettura, il calcolo del perimetro di trapezi viene utilizzato nella progettazione di strutture con forme non standard, come tetti spioventi o facciate inclinate. Gli architetti devono conoscere il perimetro per calcolare correttamente la quantità di materiale necessario e per assicurare l’integrità strutturale degli edifici.
In ingegneria civile, durante la realizzazione di ponti e strade, la forma trapezoidale è spesso presente nei sistemi di drenaggio. I perimetri di queste sezioni trapezoidali devono essere calcolati per assicurare la corretta capacità di flusso e evitare allagamenti.
Nei processi manifatturieri, il calcolo del perimetro del trapezio è utile nello sviluppo di componenti meccanici o parti di imballaggi che necessitano di precisione dimensionale. Ad esempio, serrature, cinghie, e materiali di imballaggio possono avere forme trapezoidali che richiedono calcoli precisi per garantire la loro funzionalità.
Esigenze Educative:
- Scuole: Calcolare il perimetro del trapezio è parte integrante dei programmi di matematica ed è vitale per approfondire la comprensione della geometria.
In ambito geografico e agricolo, il calcolo del perimetro del trapezio può essere utilizzato per la mappatura di terreni e per pianificare l’uso di risorse naturali o la coltivazione di campi che non hanno confini regolari.
La conoscenza e l’applicazione del perimetro di figure geometriche trapezoidali si rivelano quindi essenziali in molteplici contesti professionali, ove la precisione nelle misurazioni rappresenta un fattore critico per il successo delle attività.
Errori comuni nel calcolo del perimetro
Nel calcolare il perimetro del trapezio, alcuni errori sono frequenti e possono portare a risultati imprecisi.
Misurare in modo inesatto i lati:
Un errore frequente è la misurazione errata delle lunghezze dei lati. È essenziale che ogni lato sia misurato con precisione, soprattutto quando si tratta dei lati obliqui, noti anche come “l” e “m”.
| Lato | Errore Comune |
|---|---|
| Base Maggiore (B) | Confondere la base maggiore con quella minore e viceversa. |
| Base Minore (b) | Misurare in modo approssimativo, non tenendo conto di sporgenze o rientranze. |
| Lato obliquo (l) | Non considerare l’inclinazione del lato nel trapezio obliquo. |
| Lato obliquo (m) | Lasciarsi confondere dalla prospettiva o dall’angolazione nella misurazione. |
Non verificare l’ortogonalità:
Se i lati non sono perpendicolari, è importante considerare le reali lunghezze dei lati obliqui che possono essere più lunghi di quanto sembrino a prima vista.
Ignorare le formule corrette:
La formula per il perimetro del trapezio è la somma delle lunghezze di tutti e quattro i lati ( ![]() =
= ![]() +
+ ![]() +
+ ![]() +
+ ![]() ). Trascurare queste formule porterà a calcoli sbagliati.
). Trascurare queste formule porterà a calcoli sbagliati.
Arrotondamento prematuro:
Arrotondare i numeri durante i calcoli intermedi piuttosto che al termine può causare errori significativi. È essenziale eseguire tutti i calcoli con la massima precisione e arrotondare solo il risultato finale.
Per assicurarsi che il perimetro sia calcolato correttamente, si raccomanda di seguire queste indicazioni, prestando attenzione alle misure e alle formule impiegate.
Lezioni interattive per imparare a calcolare il perimetro
Le lezioni interattive rappresentano uno strumento efficace per l’apprendimento del calcolo del perimetro dei trapezi. Queste lezioni guidano gli studenti attraverso i passaggi del calcolo utilizzando vari metodi didattici.
Esempio pratico: Un’applicazione interattiva può presentare un trapezio con i lati etichettati e permettere agli studenti di inserire le misure. Il software calcola automaticamente il perimetro e fornisce un feedback immediato.
Importanza della visualizzazione: Le immagini interattive aiutano a comprendere come le diverse lunghezze dei lati influenzano il perimetro. Gli studenti possono modificare le lunghezze dei lati e osservare le variazioni del perimetro in tempo reale.
Inoltre, i quiz interattivi pongono domande specifiche sul calcolo del perimetro in scenari diversi, rafforzando così la capacità di applicare le formule in modo corretto.
| Attività | Descrizione |
|---|---|
| Esercizi guidati | Seguendo passo dopo passo, gli studenti apprendono la formula del perimetro del trapezio. |
| Simulazioni | Gli utenti possono manipolare forme geometriche per comprendere meglio il concetto di perimetro. |
| Giochi didattici | Rinforzano la conoscenza attraverso un approccio ludico e coinvolgente. |
Le simulazioni possono includere scenari reali che richiedono la misurazione del perimetro in contesti pratici, contribuendo così a una comprensione più profonda dell’utilità del concetto.
Lezione virtuale incentrata sulla formula del perimetro (P) del trapezio, definita come la somma della lunghezza dei quattro lati: ![]() .
.
Si raccomanda l’uso di tali applicazioni interattive per un apprendimento più efficace e coinvolgente del calcolo del perimetro del trapezio.
Matematica di base richiesta
Per calcolare il perimetro di un trapezio, si richiede la comprensione di concetti matematici fondamentali. Il perimetro è la somma delle lunghezze di tutti i lati di una figura geometrica. Per misurare correttamente il perimetro di un trapezio, è essenziale conoscere le seguenti nozioni:
Lunghezza: È la misura di uno dei lati del trapezio. Le unità di misura più comuni sono metri (m), centimetri (cm) e millimetri (mm).
Base maggiore e minore: In un trapezio, ci sono due basi parallele di lunghezze diverse; la base maggiore (B) è la più lunga, mentre la base minore (b) è la più corta.
Lati obliqui: Sono i due lati non paralleli del trapezio, generalmente indicati con le lettere c e d.
Per la corretta misurazione del perimetro, si procede con la somma delle lunghezze dei quattro lati:
![]()
Dove ![]() rappresenta il perimetro.
rappresenta il perimetro.
La conoscenza delle operazioni aritmetiche di base, come l’addizione e la sottrazione, è necessaria per eseguire il calcolo del perimetro.
Inoltre, si deve avere una dimestichezza minima con lo strumento di misura utilizzato per ottenere la lunghezza dei lati, che può essere un righello, un nastro metrico o un calibro.
| Concetto | Significato | Importanza |
|---|---|---|
| Lunghezza | Misura di un lato | Essenziale per il calcolo |
| Base maggiore e minore | Le due basi parallele | Punti di partenza del calcolo |
| Lati obliqui | Lati non paralleli del trapezio | Completa la misura del perimetro |
| Operazioni aritmetiche | Addizione e sottrazione | Necessarie per sommare i lati |
Esercizi pratici e problemi di esempio
In quest’area, si affrontano esercizi per il calcolo del perimetro del trapezio. Si ricorda che il trapezio è un quadrilatero con due lati paralleli di lunghezza diversa, definiti come base maggiore e base minore.
Esempio 1:
Data la base maggiore ![]() di 10 cm, la base minore
di 10 cm, la base minore ![]() di 6 cm, e i lati obliqui
di 6 cm, e i lati obliqui ![]() e
e ![]() di 5 cm ciascuno, calcolare il perimetro
di 5 cm ciascuno, calcolare il perimetro ![]() .
.
Formula del perimetro:![]() =
= ![]() +
+ ![]() +
+ ![]() +
+ ![]()
Calcolo:![]() = 10 + 6 + 5 + 5 = 26 cm
= 10 + 6 + 5 + 5 = 26 cm
Esempio 2:
| Elemento | Valore (cm) |
|---|---|
| Base maggiore | 14 |
| Base minore | 7 |
| Lato obliquo 1 | 4 |
| Lato obliquo 2 | 4 |
Perimetro:![]() =
= ![]() +
+ ![]() +
+ ![]() +
+ ![]()
![]() = 14 + 7 + 4 + 4 = 29 cm
= 14 + 7 + 4 + 4 = 29 cm
Il seguente elenco offre suggerimenti rapidi per il calcolo del perimetro:
- Identificare le misure di tutte le parti del trapezio.
- Utilizzare la formula corretta per sommare le lunghezze dei lati.
- Assicurarsi che tutte le misure siano nella stessa unità prima di eseguire il calcolo.
Gli esercizi includono vari livelli di difficoltà e permettono di sviluppare competenze nel calcolo dei perimetri dei trapezi nelle diverse configurazioni.