La circonferenza del cilindro rappresenta la misura lineare del bordo di una delle basi circolari dell’oggetto. Il cilindro è una figura geometrica tridimensionale composta da due basi che sono cerchi congruenti e paralleli, uniti da una superficie curva chiamata mantello. La circonferenza di uno di questi cerchi è calcolabile attraverso la formula:
Dove:
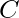indica la circonferenza
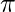è la costante pi greco, approssimativamente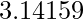 
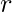rappresenta il raggio del cerchio, la distanza dal centro del cerchio al bordo
La circonferenza è essenziale per calcolare altre proprietà del cilindro come l’area di base (
), l’area laterale (
), e il volume (
), dove 
indica l’altezza del cilindro.
Utilizzare la circonferenza permette di determinare queste e altre grandezze del cilindro isotropo, il quale presenta una simmetria rotazionale attorno all’asse che congiunge i centri delle due basi. La precisa conoscenza della circonferenza è fondamentale in varie discipline, come l’ingegneria meccanica e l’architettura, per la creazione e analisi di oggetti cilindrici.
Calcolatrice circonferenza cilindro
Calcolatore Circonferenza del Cilindro
Calcolo della circonferenza del cilindro
Il calcolo della circonferenza del cilindro è una procedura matematica utilizzata per determinare la lunghezza della linea che definisce il bordo circolare delle sue basi. Questo valore è fondamentale in numerose applicazioni pratiche e teoriche.
Formula
La circonferenza di un cilindro si calcola usando la formula:
Circonferenza = 2πr
dove rappresenta il raggio della base del cilindro e è la costante pi greco, approssimativamente pari a 3,14159.
Passaggi per il calcolo
Per calcolare la circonferenza di un cilindro, seguire i seguenti passaggi:
- Misurare il raggio 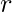della base del cilindro.
- Moltiplicare il raggio per 2 per ottenere il diametro.
- Moltiplicare il diametro ottenuto per il valore di 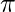(3,14159).
Questa operazione fornirà la lunghezza della circonferenza del cilindro.
Esempi numerici
Esempio 1:
- Raggio (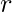): 5 cm
- Circonferenza:
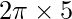cm =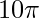 
cm ≈ 31,4159 cm
Esempio 2:
- Raggio (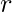): 10 cm
- Circonferenza:
cm =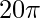 
cm ≈ 62,8318 cm
In questi esempi, la circonferenza del cilindro viene calcolata utilizzando il raggio misurato e moltiplicandolo per 2π per ottenere il valore finale.
Componenti del cilindro
Un cilindro è una figura geometrica tridimensionale costituita da due basi circolari congruenti e parallele connesse da una superficie laterale rettangolare.
Area di base
L’area di base di un cilindro è l’area di una delle due basi circolari. Si calcola moltiplicando il pi greco () per il quadrato del raggio () della base secondo la formula 
. Pertanto, se il raggio della base è 5 cm, l’area di base è 78,54 cm² (
).
Altezza del cilindro
L’altezza del cilindro è la distanza perpendicolare tra le due basi. Questa dimensione è spesso indicata con la lettera h. Nel caso di un cilindro con un’altezza di 10 cm, questa misura rappresenta la distanza verticale tra le basi circolari.
Tipi di cilindri
I cilindri possono essere classificati principalmente in due tipi: il cilindro retto e il cilindro obliquo. Questi due hanno al loro interno delle caratteristiche geometriche distinte e sotto-categorie basate sulla loro inclinazione e la forma delle basi.
Cilindro retto
Un cilindro retto è un cilindro con le basi circolari che sono parallele ed equidistanti l’una dall’altra. Tutte le linee generatrici (i segmenti che connettono i punti corrispondenti sulle due basi) sono perpendicolari alle basi e uguali in lunghezza.
- Altezza (h): Distanza tra le due basi
- Raggio (r): Distanza dal centro della base al bordo
- Area di base (A):
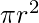
- Area laterale (Al):
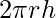
- Area totale (At):
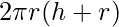
- Volume (V):
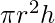
Cilindro obliquo
Il cilindro obliquo si distingue per le basi circolari che sono ancora parallele, ma le linee generatrici non sono perpendicolari alle basi. Di conseguenza, la forma del cilindro appare ‘inclinata’ rispetto al cilindro retto.
- Inclinazione (i): Angolo tra le linee generatrici e il piano della base
- Altezza (h): La perpendicolare più breve tra le due basi
- Area di base (A): Identica al cilindro retto, ossia
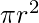
- Area laterale (Al): La superficie curva diviene più complessa a causa dell’inclinazione
- Volume (V): Uguale a quello del cilindro retto, 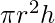, poiché le basi e l’altezza si mantengono
La determinazione dell’area laterale nel cilindro obliquo richiede considerazioni geometriche aggiuntive dovute alla sua forma inclinata.
Applicazioni pratiche della circonferenza del cilindro
La circonferenza di un cilindro ha applicazioni importanti in svariati campi, tra cui l’ingegneria, l’architettura e la produzione industriale. La circonferenza di solito si riferisce alla misura lineare del bordo di una sezione circolare del cilindro, sia essa la base o il taglio trasversale.
Ingegneria Meccanica: Gli ingegneri utilizzano la misurazione della circonferenza per progettare componenti cilindrici. Per esempio, quando si progettano motori, la circonferenza dei cilindri del motore determina importanti parametri come la quantità di combustibile iniettata e l’area della superficie su cui agiscono le forze.
- Tubi e Condotte: La circonferenza è fondamentale per calcolare la dimensione dei tubi, influenzando direttamente il loro flusso e capacità.
| Applicazione | Utilizzo della Circonferenza |
|---|---|
| Abbigliamento | Dimensionamento di elementi elastici cilindrici |
| Architettura | Progettazione di colonne e strutture portanti |
Produzione Industriale: Nelle fabbriche, le misure della circonferenza del cilindro sono fondamentali per la creazione di parti rotanti, come ingranaggi e rulli. Una precisa circonferenza è cruciale per assicurare una rotazione fluida e senza attriti.
Astronomia: La misurazione della circonferenza è utile in astronomia, per calcolare il volume e la superficie di corpi planetari e vari oggetti celesti di forma approssimativamente cilindrica.
Normative di Sicurezza: Nei contesti di salute e sicurezza, la circonferenza dei contenitori sotto pressione è vitale per assicurarsi che possano resistere alle forze interne e prevenire incidenti.
Calcolare accuratamente la circonferenza di un cilindro è quindi un’operazione matematica essenziale in molteplici contesti pratici, ogni settore ha metodi standardizzati per il calcolo in relazione alle proprie necessità specifiche.
Errori comuni nei calcoli
Quando si effettuano calcoli per la circonferenza di un cilindro, è essenziale eseguire misurazioni accurate e utilizzare correttamente i valori matematici.
Misurazione imprecisa del raggio
La precisione nel determinare il raggio è cruciale. Un errore nella misurazione del raggio può portare a un calcolo errato della circonferenza del cilindro. Si consideri la seguente tabella che evidenzia l’impatto di piccole variazioni dello stesso sul risultato finale:
| Raggio misurato (cm) | Circ. calcolata con pi greco esatto (cm) | Differenza (%) |
|---|---|---|
| 5.00 | 31.42 | – |
| 5.05 (+1%) | 31.72 | +0.96 |
| 4.95 (-1%) | 31.11 | -0.99 |
Approssimazione del pi greco
L’uso di un valore approssimativo di pi greco () può introdurre un’altra fonte di errore nei calcoli. Il valore di è irrazionale, quindi la sua rappresentazione esatta è impossibile. Tuttavia, l’utilizzo di approssimazioni comunemente impiegate (come 3.14 o 22/7) comporta variazioni rispetto al valore effettivo:
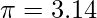: Approssimazione al centesimo più utilizzata, ma comporta un errore dello 0.05% rispetto al valore di 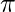(circa 3.14159).
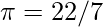: Fratto comunemente usato, genera un errore dello 0.04% rispetto al 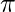reale.
È importante utilizzare una versione di quanto più accurata possibile, soprattutto in calcoli di precisione tecnica o scientifica.
Strumenti per il calcolo della circonferenza
Nel calcolo della circonferenza di un cilindro, è essenziale l’utilizzo di strumenti matematici accurati. Gli strumenti più comunemente utilizzati includono:
- Calcolatrici scientifiche: Permettono di compiere operazioni aritmetiche e funzioni trigonometriche necessarie al calcolo della circonferenza.
- Software di geometria: Offre la possibilità di inserire le dimensioni del cilindro e calcolare automaticamente la circonferenza.
Utilizzo di Calcolatrici Scientifiche
- Inserire la misura del raggio (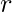) del cilindro.
- Moltiplicare il raggio per due per ottenere il diametro (
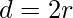). - Moltiplicare il diametro per il valore di pi greco (
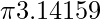) per trovare la circonferenza (
).
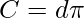Uso di Software di Geometria
- Selezionare la funzione specifica per il calcolo della circonferenza di un cilindro.
- Immettere i dati richiesti, tipicamente il raggio o il diametro.
- Il software elabora i dati e fornisce il valore della circonferenza.
Tabelle di Riferimento
In alcuni casi, si utilizzano tabelle prestampate con valori costanti di per velocizzare il calcolo della circonferenza.
Tabella per il calcolo rapido della circonferenza () con raggio ():
| raggio (r) | Circonferenza (C = 2πr) |
|---|---|
| 1 cm | 6,283 cm |
| 2 cm | 12,566 cm |
| 3 cm | 18,849 cm |
Questi strumenti assicurano precisione e velocità nel calcolo della circonferenza del cilindro, supportando sia l’apprendimento che l’applicazione professionale nel campo della geometria.
Materiali didattici per l’apprendimento
Nella didattica della geometria, specificamente quando si studia la circonferenza di un cilindro, è fondamentale disporre di materiali educativi idonei che facilitino la comprensione e l’apprendimento. I docenti possono utilizzare una varietà di strumenti e risorse che sono classificati di seguito:
Risorse Visuali
- Diagrammi: Illustrazioni dettagliate che mostrano la struttura cilindrica e i suoi componenti.
- Modelli tridimensionali: Repliche fisiche di un cilindro per osservare direttamente la forma e le dimensioni.
Supporti Testuali
- Fogli di lavoro: Documenti con esercizi pratici per calcolare la circonferenza.
- Guide: Istruzioni passo-passo su come determinare la circonferenza utilizzando la formula matematica.
Risorse Digitali
- Software educativo: Programmi che permettono la simulazione e la visualizzazione interattiva della circonferenza di un cilindro.
- Applicazioni mobili: Strumenti portatili per esercitarsi nel calcolo in qualsiasi momento e luogo.
Materiali Interattivi
- Giochi didattici: Attività ludo-educative progettate per rinforzare la conoscenza attraverso il gioco.
- Laboratori: Sessioni pratiche che permettono agli studenti di esplorare e scoprire attraverso esperimenti diretti.
L’impiego di questi materiali didattici fornisce agli studenti la possibilità di comprendere meglio concetti astratti trasformandoli in esperienze concrete. Affiancando le lezioni teoriche con tali risorse, si agevola un apprendimento più profondo della circonferenza di un cilindro.
Importanza della geometria nella vita quotidiana
La geometria è la branca della matematica che si occupa dello studio delle forme, delle dimensioni, delle figure spaziali e delle loro proprietà. Nella vita quotidiana, la geometria ha un ruolo fondamentale in molteplici aspetti, fortemente radicato nelle attività umane quotidiane.
Primo, nell’architettura e nell’ingegneria, la geometria permette di progettare edifici e strutture. Le conoscenze geometriche sono essenziali per calcolare aree e volumi, garantendo la stabilità e l’efficienza, oltre a soddisfare criteri estetici.
Secondo, la geometria trova applicazione nella navigazione e nella cartografia, permettendo di comprendere e rappresentare la Terra su mappe bidimensionali. Tali rappresentazioni sono indispensabili per viaggiare e per definire confini territoriali.
Esempi di applicazioni della geometria nella vita di ogni giorno:
- Design di interni: ottimizzare lo spazio grazie alla disposizione dei mobili.
- Cucina: calcolare la quantità degli ingredienti in base alla forma e dimensione dei contenitori.
- Tecnologia: progettazione di dispositivi elettronici utilizzando principi geometrici per massimizzare l’ergonomia e l’estetica.
La geometria, pertanto, non è soltanto una scienza astratta, ma uno strumento pratico e concreto che facilita e arricchisce la vita quotidiana, permettendo all’uomo di interagire efficacemente con l’ambiente che lo circonda e di risolvere problemi concreti con precisione e metodo.
Storia del concetto di cilindro
Il cilindro come figura geometrica ha origini antiche, risalenti alle prime civiltà che hanno studiato la geometria. Gli antichi Egizi, per esempio, erano a conoscenza della forma del cilindro e ne utilizzavano le proprietà nella costruzione di elementi architettonici.
Nel V secolo a.C., i matematici greci iniziarono a esplorare sistematicamente le proprietà dei corpi solidi, tra cui il cilindro. Un importante contributo fu dato da Euclide, che nella sua opera “Elementi” fornì una rigorosa trattazione matematica di varie figure geometriche, compresi i cilindri. Euclide definì il cilindro come un solido generato dalla rotazione di un rettangolo attorno a uno dei suoi lati.
Archimede di Siracusa (287–212 a.C.) rappresentò un altro passo fondamentale nella comprensione del cilindro. Egli dimostrò che il volume di un cilindro è uguale a quello di un prisma con la stessa altezza e area di base. Inoltre, attraverso il suo lavoro “Sulla sfera e il cilindro”, descrisse come calcolare il volume e l’area della superficie di questi solidi, stabilendo principi ancora utilizzati nell’attuale calcolo della circonferenza del cilindro.
Il Rinascimento vide un rinnovato interesse per le forme geometriche, compreso il cilindro, con matematici come Leonardo da Vinci e Luca Pacioli che contribuirono a diffondere le conoscenze matematiche greche. Questo interesse continuò durante la rivoluzione scientifica, quando matematici come Kepler e Galileo utilizzarono forme cilindriche nei loro studi sull’astronomia e sulla fisica.
Nel corso dei secoli, la comprensione del cilindro e il calcolo della sua circonferenza si sono evoluti, diventando parte integrante della matematica e della fisica moderne.
Cilindri nella natura e nella tecnologia
I cilindri sono forme geometriche che troviamo ubiquitariamente nella natura e nel costrutto umano. Nella natura si può osservare questa forma nel fusto degli alberi o nelle canne di bambù. Questi cilindri organici forniscono resistenza e flessibilità, facendo fronte agli stress meccanici come il vento e il peso della chioma.
In campo tecnologico, i cilindri sono fondamentali in molteplici applicazioni:
Motori: la maggior parte dei motori a combustione interna possiede cilindri nei quali avviene la combustione del carburante per produrre energia.
Strutture Edilizie: Colonne cilindriche, spesso in cemento armato, supportano carichi verticali garantendo stabilità agli edifici.
Stoccaggio: Serbatoi cilindrici sono spesso utilizzati per lo stoccaggio di liquidi e gas a causa della loro capacità di resistere omogeneamente alla pressione interna.
Elettrodomestici: Tubi di aspirapolveri e rulli di stampanti sono geometricamente dei cilindri per funzione e praticità di design.
In breve, il cilindro come forma si adatta perfettamente per risolvere problemi di ingegneria, ottimizzando la distribuzione di carichi e fluidi. Si possono considerare i cilindri come elementi chiave nell’avanzamento della tecnologia e nella conservazione di funzioni ecologiche.
La loro presenza ubiquitaria mostra quanto la forma cilindrica sia funzionale e versatile, soddisfando esigenze tanto naturali quanto artificiali.
