Calcolatore superficie piramide quadrata

Una piramide quadrata è un poliedro definito da una base quadrata e da quattro facce triangolari che convergono in un unico punto chiamato apice. Ogni faccia triangolare, o faccia laterale, è un triangolo isoscele la cui base coincide con un lato del quadrato di base. La piramide quadrata appartiene alla famiglia dei solidi platonici se tutte le sue facce, inclusa la base, sono poligoni regolari e congruenti fra loro – in questo caso, si parla specificamente di una piramide quadrata regolare.

Le componenti primarie di una piramide quadrata possono essere riassunte come segue:

Base: Un quadrato perfetto con quattro lati uguali, indicati come lato di base (l).
Faccia Laterale: Quattro triangoli isosceli identici, ciascuno avente come base un lato della base quadrata.
Apice: Il punto in cui si incontrano le facce laterali.
Altezza (h): Segmento perpendicolare tra la base e l’apice.
Spigolo laterale: Segmento che congiunge l’apice con ciascun vertice della base.

Per calcolare la superficie di una piramide quadrata, è necessario considerare sia l’area della base che le aree delle facce laterali. Il calcolo della superficie totale include dunque l’area del quadrato di base più le aree delle quattro facce triangolari. La formula per l’area di base (A_b) è A_b = l^2, mentre l’area di una faccia laterale (A_f) può essere generalmente espressa come A_f = (l * h_f)/2, dove h_f è l’altezza di una faccia laterale.

Calcolatore superficie piramide quadrata

Calcolo dell’area di base

La base di una piramide quadrata è costituita da un quadrato. Per il calcolo dell’area di base, è essenziale determinare la lunghezza del lato del quadrato, tipicamente indicata con la lettera a. L’area di base (A_b) di una piramide quadrata è calcolata elevando al quadrato la lunghezza del lato.

Formula dell’area di base:
$A_b = a^2$

Passaggi per il calcolo:

Misurare la lunghezza di un lato della base quadrata (a).
Moltiplicare la lunghezza del lato (a) per se stessa.

Esempio con legenda:

a: Lunghezza del lato della base quadrata (in metri).

Lato (a)	Area di base (A_b)
5 m	25 m²

In questo esempio, con un lato della base (a) di 5 metri, l’area di base (A_b) è 25 metri quadrati, risultante dalla formula A_b = a x a = 5m x 5m = 25m².

Determinazione dell’altezza della piramide

La determinazione dell’altezza di una piramide a base quadrata è un processo che coinvolge diverse formule matematiche. L’altezza ( h ) di una piramide è la distanza perpendicolare dal vertice alla base.

Formula diretta: Se sono noti il volume ( V ) della piramide e l’area ( A ) della base, l’altezza si può trovare utilizzando la seguente formula:
$h = \frac{3V}{A}$

Utilizzo della trigonometria: Se sono note l’apotema ( ap ) e il lato ( l ) della base, si può ricorrere a relazioni trigonometriche per calcolare l’altezza:

Calcolare l’apotema della base ( ab ) tramite la formula:
$ab = \frac{l}{2\sqrt{2}}$
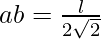
Applicare il teorema di Pitagora per trovare l’altezza ( h ):
$h = \sqrt{{ap}^2 - {ab}^2}$

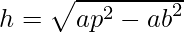
Metodo grafico: Si può disegnare un triangolo rettangolo immaginario che include l’altezza, l’apotema e l’apotema della base. Misurando quest’ultimo si può ricavare l’apotema per trovare poi l’altezza con il teorema di Pitagora.

Occorre notare che l’accuratezza del risultato dipende dalla precisione delle misure iniziali. L’analisi deve avvenire considerando errori di misurazione e possibili approssimazioni.

In assenza di altri dati, può essere necessario ricorrere a metodi di misurazione fisica per ottenere l’altezza, ad esempio mediante un altimetro o tecniche di rilievo.

Formule per il calcolo della superficie laterale

La superficie laterale di una piramide quadrata è la somma delle aree dei quattro triangoli isosceli che la compongono. Ogni triangolo ha per base un lato della base quadrata della piramide e come altezza l’apotema della piramide (un segmento perpendicolare da un vertice della base al lato opposto che passa per il punto medio).

Per calcolare l’area di un singolo triangolo laterale, si utilizza la formula:

$\text{Area triangolo} = \frac{base \cdot altezza}{2}$

Dove la base è il lato del quadrato di base (( l )) e l’altezza è l’apotema della piramide (( a )). Quindi, l’area di un solo triangolo laterale sarà:

$\text{Area triangolo} = \frac{l \cdot a}{2}$

La superficie laterale $S_{lat}$ è data dalla somma delle aree dei quattro triangoli laterali:

$S_{lat} = 4 \cdot \left( \frac{l \cdot a}{2} \right)$

Simbolo	Descrizione
( S_{lat} )	Superficie laterale
( l )	Lato della base quadrata
( a )	Apotema della piramide

La formula completa per il calcolo della superficie laterale si semplifica in:

$S_{lat} = 2 \cdot l \cdot a$

Per effettuare questo calcolo, è necessario determinare l’apotema, che a sua volta dipende dall’altezza della piramide e dalle dimensioni della base. La relazione tra apotema, altezza della piramide $h$ e metà del lato della base $\frac{l}{2}$ può essere trovata usando il teorema di Pitagora:

$a = \sqrt{h^2 + \left( \frac{l}{2} \right)^2}$

Formule per il calcolo della superficie totale

La superficie totale di una piramide a base quadrata si calcola sommando l’area della base quadrata all’area delle quattro facce triangolari laterali. Per una piramide con base quadrata di lato l e altezza laterale (apotema) a, le formule sono le seguenti:

Area della base (Ab):
$Ab = l^2 <span style="background-color: var(--wp--preset--color--base); color: var(--wp--preset--color--contrast); font-family: var(--wp--preset--font-family--body); font-size: var(--wp--preset--font-size--medium);">$
Area di una faccia laterale (Af): $Af = \frac{l \cdot a}{2}$
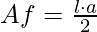
Superficie laterale (Sl):
$Sl = 4 \cdot Af$
$Sl = 4 \cdot \frac{l \cdot a}{2}$
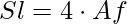
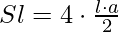
Superficie totale (St):
$St = Ab + Sl$
$St = l^2 + 4 \cdot \frac{l \cdot a}{2} <span style="background-color: var(--wp--preset--color--base); color: var(--wp--preset--color--contrast); font-family: var(--wp--preset--font-family--body); font-size: var(--wp--preset--font-size--medium);">$

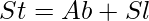
Esempio di calcolo:

Dati una piramide con lato di base l = 5 cm e apotema a = 10 cm, il calcolo sarà eseguito nel seguente modo:

Calcolare l’area di base:
$Ab = 5 cm^2 = 25 cm^2$
Determinare l’area di una faccia laterale:
$Af = \frac{5 cm \cdot 10 cm}{2} = 25 cm^2$
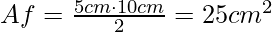
Calcolare la superficie laterale:
$Sl = 4 \cdot 25 cm^2 = 100 cm^2$
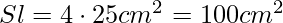
Sommare per ottenere la superficie totale:
$St = 25 cm^2 + 100 cm^2 = 125 cm^2$

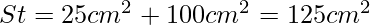
La superficie totale della piramide sarà di 125 cm^2. Queste formule permettono di calcolare facilmente la superficie di qualsiasi piramide quadrangolare data la misura della base e dell’apotema.

Esempi di calcolo della superficie totale

Una piramide a base quadrata possiede una base che è un quadrato e quattro facce laterali che sono triangoli isosceli. Per calcolare la superficie totale, occorre sommare l’area della base a quella delle quattro facce laterali.

Formula della superficie totale (S):

$S = Area\ base\ (A_b) + Area\ laterale\ (A_l)$

Dove:

$A_b = lato\ base^2$
$A_l = 4 \cdot (\frac{lato\ base \cdot altezza\ slancio}{2})$
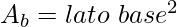
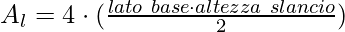
Altezza slancio è la distanza tra il centro della base quadrata e il lato obliquo.

Esempio 1:

Lato Base (lb): 6 cm
Altezza Slancio (hs): 10 cm

Calcolo:

$A_b = 6^2 = 36 cm^2$
$A_l = 4 \cdot (\frac{6 \cdot 10}{2}) = 120 cm^2$
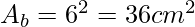
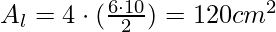
Superficie Totale (S): $36 + 120 = 156 cm^2$

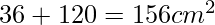
Esempio 2:

Lato Base (lb): 8 cm
Altezza Slancio (hs): 15 cm

Calcolo:

$A_b = 8^2 = 64 cm^2$
$A_l = 4 \cdot (\frac{8 \cdot 15}{2}) = 240 cm^2$
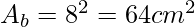
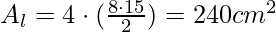
Superficie Totale (S): $64 + 240 = 304 cm^2$

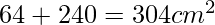
Nella tabella seguente, vengono riassunti i dati e i risultati dei calcoli:

Lato Base $lb$	Altezza Slancio $hs$	Area Base $(A_b)$	Area Laterale $(A_l)$	Superficie Totale $S$
6 cm	10 cm	36 cm²	120 cm²	156 cm²
8 cm	15 cm	64 cm²	240 cm²	304 cm²

Questi esempi mostrano come cambiamenti nelle dimensioni influenzano la superficie totale della piramide a base quadrata.

Influenza dell’inclinazione dei lati sulla superficie

L’inclinazione dei lati di una piramide quadrata ha un impatto significativo sulla sua superficie totale. La superficie totale è la somma della superficie di base e delle superfici laterali. Ogni faccia laterale è un triangolo isoscele la cui area varia in funzione dell’angolo di inclinazione.

Area della superficie di base (A_b):

La superficie di base ( A_b ) è invariata dall’inclinazione dei lati e si calcola come:

$A_b = l^2$

dove ( l ) è la lunghezza del lato della base.

Area di una faccia laterale (A_f):

Le facce laterali sono sensibili all’inclinazione. L’area di ciascuna faccia laterale ( A_f ) si calcola tramite la formula:

$A_f = \frac{l \cdot a}{2}$

dove ( l ) è la lunghezza del lato della base e ( a ) è l’altezza del triangolo isoscele (faccia laterale).

Al diminuire dell’angolo di inclinazione, l’altezza ( a ) aumenta, incrementando così l’area di ( A_f ).
In contrasto, un aumento dell’angolo di inclinazione comporta una diminuzione di ( a ), riducendo l’area di ( A_f ).

Impatto sull’area totale (A_t):

L’area totale ( A_t ) si determina con:

$A_t = A_b + 4 \cdot A_f$

Poiché la superficie di base rimane costante, variazioni nell’area totale sono direttamente proporzionali ai cambiamenti nell’area delle facce laterali dovuti all’inclinazione dei lati. Pertanto, l’area totale sarà massima quando le facce laterali sono più inclinate e minima quando l’inclinazione è minore.

Metodi approssimativi per il calcolo della superficie

Nel calcolo approssimativo della superficie di una piramide quadrata, alcuni metodi consentono di ottenere stime prossime al valore reale senza l’uso di strumenti di misura avanzati.

Metodo dei triangoli approssimati

Per stimare la superficie delle facce triangolari della piramide, può essere utilizzato il metodo dei triangoli approssimati che si basa sulla scomposizione della superficie in triangoli più semplici. Si procede calcolando l’area di ogni triangolo e sommando poi i risultati ottenuti. L’area di un triangolo si approssima utilizzando la formula:

$Area = \frac{base \times altezza}{2}$

Per ogni lato della base quadrata della piramide, si disegnano due triangoli rettangoli che hanno per altezza un’approssimazione dell’altezza della piramide stessa. La base di ciascun triangolo sarà la metà della base della piramide. Sommando l’area di questi triangoli approssimati si ottiene una stima dell’area totale delle facce laterali.

Utilizzo del Teorema di Pitagora approssimativo

Un altro metodo prevede l’applicazione di una forma approssimativa del Teorema di Pitagora per calcolare la lunghezza dell’apotema (il segmento che congiunge il centro della base della piramide al centro di una delle sue facce laterali). Sapendo che l’apotema ( a ) di una faccia triangolare è perpendicolare alla metà ( b/2 ) del lato della base, si può approssimare l’apotema con la formula:

$a \approx \sqrt{(b/2)^2 + h^2}$

dove ( h ) è l’altezza della piramide. Anche in questo caso, l’approssimazione può non essere precisa, ma fornisce una stima utile per il calcolo dell’area della superficie laterale.

Ogni metodo ha il proprio grado di approssimazione e può essere scelto in base alla precisione richiesta e agli strumenti di misura disponibili.

Differenze tra superficie laterale e totale

La superficie laterale di una piramide quadrata è la somma delle aree dei quattro triangoli che costituiscono i lati della piramide. Ciascun triangolo ha per base uno dei lati del quadrato di base della piramide e per altezza, l’apotema (la perpendicolare dal centro della base al lato del triangolo). La formula per calcolare l’area di un solo triangolo laterale è ( \frac{base \cdot apotema}{2} ). Pertanto, per ottenere la superficie laterale totale occorre sommare l’area dei quattro triangoli:

$Superficie:Laterale = 4 \times \left( \frac{base \cdot apotema}{2} \right)$

D’altra parte, la superficie totale è l’area della superficie laterale più l’area della base. La base di una piramide quadrata è un quadrato, quindi la sua area è il lato al quadrato. Segue la formula:

$Superficie:Totale = Superficie:Laterale + base^2$

Per chiarire le differenze:

Superficie Laterale: Include solo le aree delle superfici triangolari.
Superficie Totale: Comprende sia la superficie laterale che l’area della base quadrata.

Illustrando tramite una tabella:

Tipo di Superficie	Componenti
Laterale	4 aree dei triangoli laterali
Totale	Aree dei 4 triangoli laterali + area della base quadrata

In sintesi, mentre la superficie laterale esclude la base, la superficie totale la include nella sua misurazione.

Applicazioni pratiche del calcolo delle superfici piramidali

Il calcolo delle superfici piramidali trova impiego in diversi campi, dalla progettazione architettonica all’industria. Nel settore dell’edilizia, il calcolo della superficie totale di una piramide può essere essenziale per determinare la quantità di materiali da costruzione necessari e per valutare l’impatto visivo dell’opera. Un esempio specifico è il calcolo delle piastrelle richieste per coprire una facciata a forma piramidale.

In ambito archeologico, il calcolo delle superfici permette di stimare il volume di materiali impiegati nella costruzione di antiche piramidi, il che a sua volta può offrire spunti sulla logistica e le tecniche di costruzione delle civiltà passate.

Nei settori scientifici e tecnologici, le superfici piramidali vengono analizzate con l’obiettivo di ottimizzare forme e struttura, come ad esempio nelle celle fotovoltaiche a piramide, dove la superficie influisce sull’efficienza di raccolta dell’energia solare.

Campo di applicazione	Utilizzo del calcolo superficie
Edilizia	Quantità materiali, impatto visivo
Archeologia	Stima volumi e tecniche costruttive
Tecnologia	Ottimizzazione forme per efficienza

Nonostante l’apparente specificità, la capacità di calcolare con precisione le superfici piramidali supporta quindi un’ampia varietà di necessità pratiche, evidenziando l’importanza di avere competenze solide in geometria nell’applicazione reale di tali conoscenze.

Strumenti software per il calcolo della superficie

La precisione nel calcolo della superficie di una piramide quadrata è cruciale in molteplici campi, dai lavori di ingegneria all’architettura. Software dedicati forniscono strumenti specifici che permettono di effettuare questi calcoli in modo efficiente ed esatto.

Programmi CAD

Computer-Aided Design (CAD) sono programmi utilizzati primariamente da ingegneri e architetti per la modellazione digitale di oggetti tridimensionali. Essi offrono funzionalità approfondite per il calcolo delle superfici complesse, come le piramidi quadrate.

AutoCAD: capace di calcolare l’area di forme geometriche complesse con alta precisione.
SketchUp: fornisce strumenti per la modellazione 3D con la possibilità di misurare superfici e volumi.

Applicazioni mobili

Le applicazioni per smartphone e tablet consentono di effettuare il calcolo della superficie di una piramide quadrata in maniera pratica e rapida, direttamente dal cantiere o in movimento.

GeoGebra 3D: permette la creazione di modelli 3D e il calcolo delle relative superfici.
AutoCAD mobile app: adatta per l’uso in loco, consente di calcolare le aree e condividere i risultati.

Fogli di calcolo

I fogli di calcolo, come Microsoft Excel o Google Fogli, possono essere programmati per eseguire calcoli di superficie inserendo formule matematiche specifiche.

Excel:
- Vantaggio: Ampia gamma di strumenti per la modellistica matematica.
- Utilizzo: Creazione di formule personalizzate per il calcolo della superficie di piramidi quadrate.
Google Fogli:
- Vantaggio: Accessibilità e condivisione in tempo reale.
- Utilizzo: Impiego di fogli di calcolo condivisi per collaborazioni a distanza.

Errori comuni nel calcolo delle superfici delle piramidi

Calcolare la superficie di una piramide quadrata richiede precisione, e alcuni errori sono comuni tra chi si approccia a questo compito.

Confusione tra superficie laterale e totale: La superficie laterale è data dalla somma delle aree dei triangoli che costituiscono le facce inclinate, mentre la superficie totale è la somma della superficie laterale e dell’area della base quadrata. Spesso si dimentica di aggiungere l’area della base nel calcolo finale.

Superficie laterale: A_l = perimetro_base * altezza_apotema / 2
Superficie totale: A_t = A_l + area_base

Errore nel calcolo dell’altezza apotema: L’apotema di una faccia di una piramide quadrata è la distanza dalla base al vertice della faccia triangolare. Una misura errata dell’altezza apotema porta a un calcolo scorretto delle superfici.

Misurazione non accurata dei lati: La base della piramide deve avere tutti e quattro i lati identici. Misure imprecise dei lati creano discrepanze tra i valori attesi e calcolati dell’area della base.

Uso improprio delle formule: Utilizzare le formule geometriche inappropriate, come quelle destinate a piramidi con basi non quadrate, porta a risultati erronei.

Errore	Conseguenza
Omissione area della base	Superficie totale sottostimata
Altezza apotema errata	Area delle facce laterali incorretta
Lati della base inaccurati	Area della base e perimetro non corretti
Formule errate	Calcolo generale invalido

Per evitare questi errori, è cruciale la verifica delle misurazioni e l’applicazione corretta delle formule specifiche per le piramidi quadrate.

Calcolatore superficie piramide quadrata

Calcolatore superficie piramide quadrata

Calcolo dell’area di base

Determinazione dell’altezza della piramide

Formule per il calcolo della superficie laterale

Formule per il calcolo della superficie totale

Esempi di calcolo della superficie totale

Influenza dell’inclinazione dei lati sulla superficie

Metodi approssimativi per il calcolo della superficie

Metodo dei triangoli approssimati

Utilizzo del Teorema di Pitagora approssimativo

Differenze tra superficie laterale e totale

Applicazioni pratiche del calcolo delle superfici piramidali

Strumenti software per il calcolo della superficie

Programmi CAD

Applicazioni mobili

Fogli di calcolo

Errori comuni nel calcolo delle superfici delle piramidi

Piedi metri: conversione

Il calcolo del “codice fiscale diretto”

Conversione da piedi a cm (e da cm a pollici)

Leave a Reply Cancel Reply

Chi siamo

Privacy Policy

Termini di servizio

Cookie policy

Contattaci

CALCOLO.ONLINE