La distanza euclidea rappresenta il metodo più diretto per misurare la distanza tra due punti nello spazio euclideo. Questa distanza è definita come la lunghezza del segmento più breve che connette due punti.
Nella geometria bidimensionale, viene calcolata utilizzando il teorema di Pitagora.
Per due punti ![]() e
e ![]() , la formula della distanza euclidea
, la formula della distanza euclidea ![]() è:
è:
![]()
Questa formula si estende a spazi di dimensioni superiori. Per esempio, nello spazio tridimensionale, la formula include anche la coordinata ![]() :
:
![]()
In generale, in uno spazio euclideo a ![]() dimensioni
dimensioni ![]() , la distanza euclidea tra due punti
, la distanza euclidea tra due punti ![]() e
e ![]() , aventi coordinate
, aventi coordinate ![]() e
e ![]() , rispettivamente, è data da:
, rispettivamente, è data da:
![]()
Il calcolo della distanza euclidea trova applicazioni pratiche in vari campi come la fisica, l’ingegneria, e l’analisi dei dati. È fondamentale nell’elaborazione delle informazioni digitali, come nell’elaborazione delle immagini e nella computer grafica, dove rappresenta la distanza tra i pixel o tra i modelli geometrici.
Calcolatore distanza euclidea
Calcolatore Distanza Euclidea in 2D
Calcolatore Distanza Euclidea in 3D
Applicazioni Pratiche
Il calcolatore della distanza euclidea è uno strumento fondamentale in molteplici campi tecnologici e scientifici, permettendo di quantificare la similitudine o la differenza tra dati multidimensionali.
Scienza dei Dati
In scienza dei dati, la distanza euclidea è impiegata per valutare e confrontare punti dati all’interno di uno spazio multidimensionale. Viene utilizzata principalmente nei processi di clustering, come l’algoritmo K-means, per raggruppare dati simili.
La distanza euclidea, definita come ![]() , offre una misurazione diretta della distanza tra i punti.
, offre una misurazione diretta della distanza tra i punti.
Esempi pratici:
- Classificazione dei clienti: Raggruppamento dei clienti basato sulle loro abitudini di acquisto.
- Analisi genetica: Confronto di sequenze genetiche per identificare similitudini o discordanze.
Computer Vision
Nel campo della computer vision, la distanza euclidea è spesso applicata per confrontare le caratteristiche visive estratte dalle immagini. Questa metrica è vitale per sistemi di riconoscimento facciale e di oggetti, dove la distanza tra le features estratte gioca un ruolo critico nell’identificazione e classificazione delle immagini.
Esempi pratici:
- Riconoscimento facciale: Distanza tra caratteristiche facciali per verificare l’identità di una persona.
- Controllo qualità: Ispezione automatica di parti manifatturiere per rilevare difetti, confrontando caratteristiche con un modello di riferimento standard.
Calcolo della Distanza Euclidea
Il calcolo della distanza euclidea permette di determinare la distanza più breve tra due punti in uno spazio di qualsiasi numero di dimensioni. Questa misurazione è spesso utilizzata in vari campi come la matematica, fisica e nell’informatica, in particolare nell’ambito dell’apprendimento automatico e nell’analisi multidimensionale dei dati.
Formula bidimensionale
Per calcolare la distanza euclidea in uno spazio bidimensionale, si utilizza la formula seguente:
![]()
dove ![]() rappresenta la distanza euclidea tra i punti
rappresenta la distanza euclidea tra i punti ![]() e
e ![]() , mentre
, mentre ![]() e
e ![]() sono le coordinate dei punti rispettivamente in uno spazio a 2 dimensioni.
sono le coordinate dei punti rispettivamente in uno spazio a 2 dimensioni.
Formula tridimensionale
Per calcolare la distanza euclidea in uno spazio tridimensionale, la formula si estende per includere un’ulteriore dimensione:
![]()
Qui, ![]() indica la distanza tra i punti
indica la distanza tra i punti ![]() e
e ![]() , e
, e ![]() e
e ![]() sono le rispettive coordinate dei punti in tre dimensioni.
sono le rispettive coordinate dei punti in tre dimensioni.
Formula generale per spazi n-dimensionali
In spazi con più di tre dimensioni, la formula della distanza euclidea diventa:
![]()
In questa formula, ![]() rappresenta il numero di dimensioni dello spazio, mentre
rappresenta il numero di dimensioni dello spazio, mentre ![]() e
e ![]() sono le coordinate dei punti
sono le coordinate dei punti ![]() e
e ![]() nella i-esima dimensione.
nella i-esima dimensione.
Implementazione in software
Il calcolo della distanza euclidea è un’operazione matematica che viene frequentemente implementata in vari linguaggi di programmazione per scopi quali la grafica computerizzata, l’analisi dati e l’apprendimento automatico.
Python
In Python, il calcolo della distanza euclidea può essere eseguito utilizzando la libreria math. Esempio di codice:
import math
def distanza_euclidea(punto1, punto2):
return math.sqrt(sum((val1 - val2) ** 2 for val1, val2 in zip(punto1, punto2)))
Punto1 e punto2 sono tuple o liste che rappresentano coordinate nello spazio.
JavaScript
JavaScript non include una libreria matematica standard così completa come Python, ma il calcolo può essere comunque realizzato con facilità. Esempio di codice:
function distanzaEuclidea(punto1, punto2) {
return Math.sqrt(punto1.reduce((sum, val, index) => {
return sum + Math.pow(val - punto2[index], 2);
}, 0));
}
punto1 e punto2 sono array che contengono le coordinate dei punti.
C++
C++ è un linguaggio di programmazione ampiamente utilizzato che fornisce funzionalità di basso livello per il calcolo efficiente. Ecco un esempio di implementazione della distanza euclidea:
#include <cmath>
#include <vector>
double distanzaEuclidea(const std::vector<double>& punto1, const std::vector<double>& punto2) {
double sum = 0.0;
for(size_t i = 0; i < punto1.size(); i++) {
sum += std::pow(punto1[i] - punto2[i], 2);
}
return std::sqrt(sum);
}
punto1 e punto2 sono std::vector che memorizzano le coordinate dei punti.
Ottimizzazione del Calcolo
L’ottimizzazione del calcolo della distanza euclidea si concentra sull’aumento dell’efficienza e della rapidità mediante l’utilizzo di algoritmi ottimizzati e librerie specializzate.
Algoritmi Efficienti
Gli algoritmi efficienti sono essenziali per accelerare il calcolo della distanza euclidea, soprattutto quando si lavora con grandi dataset. Un esempio è l’algoritmo di Strassen per la moltiplicazione di matrici, che riduce la complessità computazionale rispetto all’algoritmo standard.
Un’altra tecnica è l’uso della programmazione dinamica per memorizzare e riutilizzare risultati intermedi, minimizzando così il numero di calcoli necessari.
Uso di Librerie Specializzate
L’impiego di librerie specializzate può notevolmente semplificare e velocizzare il calcolo. Librerie come NumPy per Python offrono funzioni ottimizzate per il calcolo vettoriale e matriciale che sono fondamentali nella determinazione delle distanze euclidee.
Di seguito un esempio di come viene impiegata una funzione di NumPy:
- Importazione della libreria NumPy:
import numpy as np - Calcolo della distanza euclidea:
vettore1 = np.array([x1, y1]) vettore2 = np.array([x2, y2]) distanza = np.linalg.norm(vettore1 - vettore2)
Distanza euclidea normalizzata
La distanza euclidea normalizzata è una variante della distanza euclidea tradizionale.
Viene utilizzata per misurare la similarità tra due punti in spazi con variabili che hanno scale diverse.
La distanza euclidea normalizzata viene calcolata normalizzando ciascuna dimensione dei punti dati prima di calcolare la loro distanza euclidea.
La formula per la distanza euclidea normalizzata tra due punti ![]() e
e ![]() nel contesto di un insieme di dati
nel contesto di un insieme di dati ![]() con
con ![]() dimensioni è data da:
dimensioni è data da:
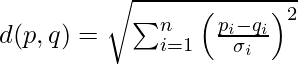
dove:
-
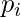 e
e 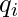 sono le coordinate dei punti nelle dimensioni
sono le coordinate dei punti nelle dimensioni 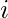 ,
, -
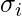 è la deviazione standard delle coordinate nella dimensione
è la deviazione standard delle coordinate nella dimensione 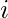 .
.
Questa metrica è particolarmente utile quando le dimensioni hanno unità di misura diverse o variano in ampiezze.
Normalizzare le distanze permette di renderle confrontabili e di evitare che variabili con scala maggiore influenzino in modo eccessivo il calcolo della distanza.
Come si effettua la normalizzazione:
- Calcolare la media
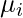 e la deviazione standard
e la deviazione standard 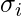 per ognuna delle
per ognuna delle 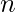 dimensioni.
dimensioni. - Sottrarre la media dal valore di ogni dimensione e dividere il risultato per la deviazione standard corrispondente.
- Calcolare la distanza euclidea con i valori normalizzati.
Differenze con altre metriche di distanza
La distanza euclidea è una misura di spazio geometrico conosciuta per la sua applicazione nel calcolo della distanza più breve tra due punti in uno spazio multidimensionale.
Questa metrica differisce da altre nel modo in cui valuta la distanza.
Distanza di Manhattan
La distanza euclidea calcola la distanza diretta tra due punti utilizzando il teorema di Pitagora, risultando in un percorso diagonale in uno spazio bidimensionale o una linea retta in uno spazio tridimensionale.
Al contrario, la distanza di Manhattan, conosciuta anche come distanza del taxi o norma L1, si basa sul calcolare la distanza sommando il valore assoluto delle differenze delle coordinate dei punti.
- Differenze Principali:
- Traiettoria:
- Euclidea – percorso più breve; diagonale
- Manhattan – somma dei movimenti orizzontali e verticali
- Applicazioni:
- Euclidea – spazi continui
- Manhattan – griglie, circuiti integrati, sistemi di strade urbani
- Traiettoria:
Distanza di Chebyshev
Analogamente, mentre la distanza euclidea misura il segmento più breve tra due punti, la distanza di Chebyshev (o norma L∞) si concentra sulla massima differenza assoluta tra le coordinate di questi punti.
- Differenze Principali:
- Principio:
- Euclidea – distanza come l’ipotenusa tra due punti
- Chebyshev – massima differenza sulle singole dimensioni
- Contesto:
- Euclidea – uso generale in spazi euclidei
- Chebyshev – giochi di strategia, progettazione di microprocessori, matematica discreta
- Principio:
Casistiche di Errore Comuni nella Computazione
Durante il calcolo della distanza euclidea, possono emergere diversi errori influenzando l’accuratezza del risultato.
Errori nei dati di input:
- Valori Mancanti: Uno o più valori coordinate non sono forniti.
- Valori Errati: Coordinate con valori inesatti o al di fuori del dominio previsto.
- Formato Inconciliabile: Coordinate fornite in formati non compatibili, come la miscelazione di gradi con radianti.
Errore di interpretazione della formula:
- Errata Applicazione: Misapplicazione della formula di distanza
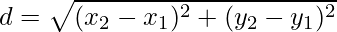 dove
dove 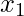 ,
, 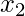 ,
, 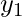 ,
, 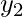 sono le coordinate dei due punti in uno spazio bidimensionale.
sono le coordinate dei due punti in uno spazio bidimensionale. - Calcolo Sbagliato: Errori aritmetici nel calcolo delle differenze o delle radici quadrate.
- Trascuranza Delle Dimensioni: Ignorare il fatto che la formula base si applica solo a uno spazio bidimensionale e non è direttamente estendibile a dimensioni superiori senza modifiche.
Errori software e hardware:
- Precisione Numerica Limitata: Limitazioni della rappresentazione dei numeri nei calcoli informatici possono causare discrepanze.
- Malfunzionamenti Hardware: Guasti all’hardware o sovraccarichi di sistema possono compromettere l’esecuzione del calcolo.
Errori umani:
- Misinterpretazione dei Risultati: Interpretazione errata dei risultati numerici a causa di confusione o ignoranza delle proprietà metriche dello spazio euclideo.
- Errori di Trascrizione: Inserimento incorretto di valori dovuto a sviste o superficialità.
Esercizi pratici
La distanza euclidea è una misura matematica che esprime la lunghezza del segmento più breve che congiunge due punti in uno spazio euclideo.
Per praticare il calcolo della distanza euclidea in due dimensioni, si considerino i seguenti punti A e B con le rispettive coordinate:
- Punto A: (
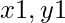 )
) - Punto B: (
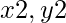 )
)
La formula per la distanza euclidea ![]() tra due punti è:
tra due punti è:
![]()
Esercizio 1: Data la coppia di punti A(1, 2) e B(4, 6), si utilizzi la formula per calcolare la distanza euclidea.
Esercizio 2: Si considerino i punti C(-3, -2) e D(2, 1). Si applichi la formula per determinare la distanza tra C e D.
Esempio di soluzione: Per l’Esercizio 1, la sostituzione delle coordinate nella formula fornisce:
![]()
Dunque, la distanza euclidea tra i punti A e B è 5 unità.
Estensioni alla distanza euclidea
Le estensioni alla distanza euclidea rappresentano una parte cruciale del calcolo delle distanze in spazi multidimensionali e nell’ambito dell’apprendimento automatico.
Offrono maggiore flessibilità e adattabilità in diversi scenari e contesti specifici.
Distanza ponderata
La distanza ponderata introduce dei pesi individuali per le dimensioni considerate nel calcolo della distanza euclidea, per riflettere l’importanza relativa di ciascuna di esse.
La formula si modifica come segue, dove (w_i) denota il peso assegnato alla (i)-esima dimensione:
![]()
Ad esempio, se si considera un punto ![]() e un punto
e un punto ![]() in uno spazio bidimensionale con pesi
in uno spazio bidimensionale con pesi ![]() e
e ![]() la distanza ponderata sarà:
la distanza ponderata sarà:
![]()
Distanza euclidea quadratica
La distanza euclidea quadratica, nota anche come distanza di Mahalanobis, si differenzia dalla distanza euclidea standard per il fatto di tenere in considerazione la covarianza tra le variabili.
La sua formula generale è:
![]()
dove ![]() rappresenta la matrice di covarianza.
rappresenta la matrice di covarianza.
Questa distanza misura l’effettiva separazione statistica tra due punti in uno spazio che tiene conto della correlazione tra le variabili.
Ad esempio, considerando due punti ![]() e
e ![]() e la matrice di covarianza
e la matrice di covarianza ![]() :
:
![]()
questa distanza sarà minore se i punti si trovano lungo l’asse con maggiore varianza e maggiore lungo quello con minore varianza.
FAQ inerenti al Calcolatore della Distanza Euclidea
Che cos’è il Calcolatore della Distanza Euclidea? Il Calcolatore della Distanza Euclidea è uno strumento matematico che misura la distanza lineare tra due punti nello spazio euclideo. La formula per calcolarla coinvolge le coordinate di questi punti.
Come si calcola la distanza euclidea? Per calcolare la distanza euclidea d tra due punti A e B con coordinate (x₁, y₁) e (x₂, y₂), si utilizza la seguente formula: d = √[(x₂ - x₁)² + (y₂ - y₁)²].
| Punto A | Punto B | Formula Distanza Euclidea |
|---|---|---|
| (x₁, y₁) | (x₂, y₂) | d = √[(x₂ - x₁)² + (y₂ - y₁)²] |
Quali applicazioni impiegano il Calcolatore della Distanza Euclidea? Il Calcolatore viene impiegato in diverse discipline come l’analisi dei dati, la statistica, l’ingegneria e la geometria computazionale.
È possibile calcolare la distanza euclidea in spazi con più di due dimensioni? Sì, la formula si estende a spazi n-dimensionali sommando i quadrati delle differenze per ogni dimensione aggiuntiva.