La radice quadrata di un numero è un valore che, moltiplicato per se stesso, dà come risultato il numero originale. Si rappresenta con il simbolo √, che si premette al numero dal quale si vuole estrarre la radice quadrata. Per esempio, la radice quadrata di 64, denotata come √64, è 8, poiché 8 × 8 = 64.
Per numeri non negativi, vi è sempre una radice quadrata reale e non negativa, detta radice quadrata principale, e una negativa. Per esempio, √64 può essere sia +8 che -8, ma comunemente si fa riferimento al valore positivo.
I seguenti sono alcuni punti chiave associati alla radice quadrata:
- Unicità: Ogni numero positivo ha una sola radice quadrata principale.
- Numeri interi: Se la radice quadrata di un numero è un numero intero, allora viene chiamata quadrato perfetto.
- Numeri reali: Tutti i numeri reali positivi hanno radici quadrate reali, mentre i numeri negativi non hanno radici quadrate nel campo dei numeri reali.
Qui si presenta una tabella che elenca alcune radici quadrate di base:
| Numero | Radice Quadrata |
|---|---|
| 1 | 1 |
| 4 | 2 |
| 9 | 3 |
| 16 | 4 |
| 64 | 8 |
È importante notare che nel contesto dei numeri complessi, anche i numeri negativi hanno radici quadrate. In tale contesto, la radice quadrata di -64 sarebbe 8i, dove i rappresenta l’unità immaginaria, definita tale che i² = -1.
Calcolo della radice quadrata di 64
Il termine radice quadrata si riferisce all’operazione matematica volta a trovare un numero che, moltiplicato per se stesso, dia come risultato il numero dato. Nel caso del numero 64, il calcolo della radice quadrata è particolarmente semplice perché 64 è un quadrato perfetto.
La radice quadrata di 64 si rappresenta con il simbolo √64 e il suo valore è 8. Questo risultato si ottiene perché 8 × 8 = 64. L’operazione può essere schematizzata nella seguente tabella:
| Numero | Radice Quadrata | Risultato |
|---|---|---|
| 64 | √64 | 8 |
Per ulteriori chiarimenti, si può considerare anche l’approccio sistematico per trovare la radice quadrata di un numero tramite il metodo di approssimazione o utilizzando lo sviluppo in serie.
Nell’insegnamento matematico, il calcolo della radice quadrata di un quadrato perfetto come 64 è spesso utilizzato come esempio introduttivo per comprendere il concetto di radice quadrata e per abituare gli studenti con il processo di fattorizzazione.
Si deve notare che il numero 64 ha anche una radice quadrata negativa, poiché (-8) × (-8) = 64. Pertanto, si può affermare che ±8 sono entrambe radici quadrate di 64. Tuttavia, quando si parla di “la radice quadrata” senza ulteriore specificazione, si fa riferimento al valore positivo.
La radice quadrata di un numero trova applicazioni pratiche in vari campi, come l’algebra, la geometria e anche in contesti pratici come il calcolo di aree o l’estrazione di informazioni da dati statistici.
Calcolatore Radice Quadrata
Applicazioni pratiche della radice quadrata di 64
La radice quadrata di 64, che è uguale a 8, ha varie applicazioni pratiche nei settori matematico, ingegneristico, architettonico e educativo.
Matematica e educazione:
- Misurazione: Nell’insegnamento delle misure, è comune utilizzare esempi con la radice quadrata per calcolare il lato di un quadrato che ha un’area di 64cm².
- Concetti geometrici: Si insegna agli studenti che la radice quadrata di un numero corrisponde alla lunghezza del lato di un quadrato con un’area equivalente.
Ingegneria:
- Design strutturale: In ingegneria strutturale, può essere necessario calcolare la radice quadrata di un numero durante il dimensionamento degli elementi di una struttura.
- Calcoli elettrici: Nell’ingegneria elettrica, potrebbero utilizzare la radice quadrata per calcolare l’intensità di corrente in circuiti con potenza pari a 64 watt.
Architettura:
- Pianificazione dello spazio: In architettura, quando si pianificano spazi quadrati con un certo numero di aree, si può utilizzare la radice quadrata per determinare la lunghezza dei lati di una stanza a partire dalla sua area.
- Disegno tecnico: Gli architetti possono applicare la radice quadrata nel disegno tecnico quando lavorano con piani che includono quadrati perfetti di area nota.
L’apprendimento e l’utilizzo della radice quadrata di 64 nelle diverse applicazioni aiutano a sviluppare una profonda comprensione di questa operazione matematica e della sua rilevanza nel mondo reale.
Radice quadrata nel contesto matematico
La radice quadrata, nell’ambito della matematica, è un’operazione che consente di trovare un numero che, moltiplicato per se stesso, fornisce come prodotto il numero dato. Per il numero 64, la radice quadrata è 8, poiché 
. Questa operazione è rappresentata dal simbolo 
.
Proprietà fondamentali:
- Unicità: Ogni numero positivo ha una sola radice quadrata positiva.
- Operazione inversa: La radice quadrata è l’operazione inversa dell’elevamento al quadrato.
Usi pratici:
- Calcolo in geometria: Determinazione della lunghezza del lato di un quadrato con area nota.
- Algebra: Risoluzione di equazioni di secondo grado.
Tabella di radici quadrate comuni:
| Numero | Radice quadrata |
|---|---|
| 1 | 1 |
| 4 | 2 |
| 9 | 3 |
| 16 | 4 |
| 25 | 5 |
| 36 | 6 |
| 49 | 7 |
| 64 | 8 |
| 81 | 9 |
| 100 | 10 |
Nel risolvere problemi pratici e teorici, il calcolo della radice quadrata è uno strumento essenziale. Ad esempio, in fisica, può essere impiegata per calcolare l’intensità di una forza o la lunghezza di un’onda. In informatica, algoritmi che implementano la radice quadrata giocano un ruolo chiave in numerosi processi computazionali.
Metodi di approssimazione per radici quadrate
Per calcolare la radice quadrata di un numero senza l’uso di calcolatrici, si possono adottare diversi metodi di approssimazione. Uno di questi è il Metodo di Babilonia o Metodo di Erode, che consiste nell’eseguire una serie di iterazioni a partire da una stima iniziale.
- Stima Iniziale: Si parte scegliendo un numero che si crede sia vicino alla radice quadrata del numero di interesse.
- Iterazione:
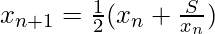
dove 
è il numero di cui si vuole calcolare la radice quadrata e 
è la stima all’n-esima iterazione.
Un altro metodo è quello di approssimazione per eccesso e difetto, che implica trovare due numeri, uno leggermente maggiore e l’altro leggermente inferiore, che moltiplicati producano il numero desiderato. La media di questi due numeri fornisce un’approssimazione della radice quadrata.
Inoltre, esiste il metodo delle frazioni continue, che trasforma la radice quadrata in una successione di frazioni. Questo metodo può essere complesso e meno intuitivo, ma è molto accurato per alcune classi di numeri.
Ecco un esempio di iterazione per il Metodo di Babilonia per approssimare la radice quadrata di 64:
| Iterazione | Stima | Equazione |
|---|---|---|
| 1 | 8 |  |
| 2 | 8 |  |
| … | … | … |
Si può notare che nel caso della radice quadrata di 64, il metodo converge rapidamente alla risposta esatta, che è 8.
L’efficacia di questi metodi varia a seconda del numero e della precisione richiesta; il Metodo di Babilonia è generalmente efficace per la maggior parte dei calcoli quotidiani non professionistici.
Storia del concetto di radice quadrata
La radice quadrata, indicata con il simbolo √, rappresenta una delle operazioni fondamentali nell’ambito della matematica. In particolare, la radice quadrata di un numero x è quel numero che, elevato al quadrato, dà come risultato x.
L’origine del concetto di radice quadrata risale agli antichi Sumeri, circa 4000 anni fa, ma sono stati gli antichi babilonesi a sviluppare un metodo sistematico per calcolare le radici quadrate di numeri interi e l’approssimazione di quelle di numeri non quadrati perfetti. Gli Egizi, attraverso il Papiro di Ahmes, conosciuto anche come il Papiro Rhind (1650 a.C. circa), ci hanno lasciato prove della conoscenza delle radici quadrate per risolvere problemi pratici di geometria.
Durante il tempo dei Greci, matematici come Euclide e Archimede hanno approfondito lo studio delle radici quadrate con metodi geometrici. Il loro lavoro è stato ulteriormente sviluppato nei secoli successivi da matematici indiani come Brahmagupta, il quale nel VII secolo ha introdotto regole negative e ha dato una formulazione più completa alla soluzione delle equazioni quadratiche includendo anche le radici quadrate.
Il simbolo attuale della radice quadrata (√) venne introdotto solo nel 1525 dal matematico tedesco Christoph Rudolff. La forma del simbolo ha una possibile derivazione dal carattere “r”, iniziale di “radix”, che in latino significa radice.
Con il passare dei secoli, l’algebra moderna ha definito e ampliato il concetto di radice quadrata per includere i numeri non reali e il concetto di radice quadrata di numeri negativi ha portato allo sviluppo dei numeri complessi.
L’importanza delle radici quadrate in algebra
Le radici quadrate sono operazioni matematiche fondamentali in algebra. Rappresentano l’operazione inversa dell’elevamento al quadrato. Ad esempio, la radice quadrata di 64 è 8, perché 
. Questa operazione è essenziale per molte applicazioni e concetti matematici.
Applicazioni Pratiche:
- Risoluzione di equazioni: Si utilizzano le radici quadrate per risolvere equazioni di secondo grado.
- Misurazioni: Le radici quadrate sono usate nelle formule per calcolare distanze, aree e volumi.
Un esempio di equazione di secondo grado:
In algebra, l’analisi delle funzioni include spesso l’identificazione dei punti in cui le funzioni intersecano gli assi, e le radici quadrate sono essenziali per questo tipo di calcoli. Le radici quadrate consentono di esprimere in forma più semplice le radici di equazioni polinomiali. Sono anche cruciali per la normalizzazione di numeri durante la semplificazione di espressioni algebriche.
L’impiego di radici quadrate è fondamentale anche per l’avanzamento in aree più complesse della matematica, come l’algebra lineare e l’analisi complessa. Senza una comprensione solida delle radici quadrate, gli studenti avrebbero difficoltà nel progredire oltre i concetti algebrici basilari.
Esempi di Formule Che Richiedono la Radice Quadrata:
- Teorema di Pitagora:
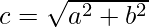
- Formula della distanza:
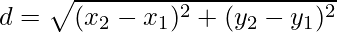
In ambito accademico e professionale, la conoscenza delle radici quadrate è una competenza matematica essenziale, impiegata sia in contesti teorici che pratici.
La radice quadrata di 64 in geometria
In geometria, la radice quadrata si riferisce al valore che, moltiplicato per se stesso, produce un dato numero. La radice quadrata di 64 è 8, poiché 8 x 8 = 64. Questo concetto è fondamentale in numerose applicazioni geometriche.
Per esempio, considerando un quadrato con un’area di 64 unità quadrate, la lunghezza di ogni lato del quadrato è la radice quadrata dell’area. In questo caso, ogni lato del quadrato misura 8 unità. Questo è illustrato nella seguente tavola:
| Area (unità quadrate) | Lunghezza del lato (unità) |
|---|---|
| 64 | 8 |
La radice quadrata di 64 può essere rappresentata anche in termini di diagonali. In un quadrato, la lunghezza della diagonale (d) può essere trovata utilizzando il teorema di Pitagora, 
, dove L rappresenta la lunghezza del lato del quadrato. Da questo, si deduce che la diagonale di un quadrato con un’area di 64 unità quadrate è 
, approssimativamente 11.31 unità.
La comprensione della radice quadrata di 64 è essenziale nello studio di figure e spazi tridimensionali. In un cubo con un volume di 512 unità cubiche, il calcolo del lato richiede l’estrazione della radice cubica. Tuttavia, se si conosce la superficie di una delle facce del cubo (64 unità quadrate), la radice quadrata di tale superficie rivela immediatamente la misura del lato (8 unità), semplificando così il calcolo del volume o di altre proprietà correlate.
Radici quadrate e teoria dei numeri
La radice quadrata di un numero è un valore che, moltiplicato per se stesso, restituisce il numero originale. La radice quadrata di 64 è 8, perché . In teoria dei numeri, lo studio delle radici quadrate è fondamentale perché interseca diversi concetti, tra cui la fattorizzazione dei numeri interi e l’analisi dei numeri primi.
Proprietà delle radici quadrate:
- Integralità: Una radice quadrata può essere o un numero intero o irrazionale, mai un frazionamento.
- Unicità: Ogni numero non negativo ha una sola radice quadrata positiva.
| Numero | Radice Quadrata |
|---|---|
| 64 | 8 |
| 49 | 7 |
| 36 | 6 |
| 25 | 5 |
Nel contesto dei numeri interi, una radice quadrata intera emerge solo quando il numero è un quadrato perfetto, ossia il prodotto di un intero per se stesso. Ad esempio, 64 è un quadrato perfetto di 8.
Inoltre, la decomposizione in fattori primi di un numero gioca un ruolo cruciale nell’identificazione delle sue radici quadrate. La somma dei gradi dei fattori primi della fattorizzazione deve essere pari perché il numero sia un quadrato perfetto.
Esempi di fattorizzazione e radici quadrate:
→ 
→ 
.
→ 
→ 
.
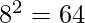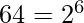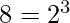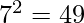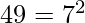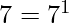Il calcolo della radice quadrata ha impatto su aree come la crittografia, innanzitutto nella fattorizzazione dei grandi numeri utilizzati nelle chiavi pubbliche. Qui, la complessità computazionale di determinare le radici quadrate di numeri molto grandi è sfruttata per assicurare la sicurezza delle informazioni.
Software e calcolatrici per radici quadrate
Numerosi software matematici e calcolatrici digitali sono progettati per calcolare la radice quadrata di numeri. Questi strumenti sono essenziali per gli studenti, ingegneri e professionisti che necessitano di risultati rapidi e precisi.
| Software/Calcolatrice | Funzionalità |
|---|---|
| Microsoft Excel | Utilizza la funzione =RADQ(numero) per ottenere la radice quadrata. |
| Wolfram Alpha | Ricerca online che fornisce risultati dettagliati per il calcolo delle radici quadrate. |
| Calcolatrici scientifiche | La maggior parte include un tasto √ per calcolare direttamente la radice quadrata. |
| Python | Linguaggio di programmazione con la funzione math.sqrt(numero) nel modulo math. |
Le applicazioni mobili come Calculator+ e Desmos Graphing Calculator forniscono anche funzionalità per il calcolo delle radici quadrate. Molti siti web offrono calcolatrici gratuite che possono essere usate senza installare alcun software.
L’utilizzo di questi strumenti comporta l’inserimento del numero di cui si desidera calcolare la radice quadrata e la pressione del pulsante appropriato. Il risultato viene generato istantaneamente. Ad esempio, inserendo il numero 64 in una di queste calcolatrici, si riceverà 8 come risultato, poiché 8 al quadrato è 64.
Insegnamento della radice quadrata nella matematica scolastica
L’introduzione della radice quadrata si verifica tipicamente nelle classi di matematica di livello intermedio. Gli studenti apprendono che la radice quadrata è l’operazione inversa dell’elevamento al quadrato. Ad esempio, dato un numero positivo A, la radice quadrata di A è quel numero che, moltiplicato per se stesso, dà come risultato A.
Inizialmente, gli insegnanti spesso presentano radici quadrate di numeri quadrati perfetti, quali 4, 9, 16, per costruire familiarità con il concetto attraverso esempi chiari. Il valore della radice quadrata di 64, per esempio, è 8, poiché .
Strategies for Teaching Square Roots
| Concetto | Strategia Didattica |
|---|---|
| Concetto di radice | Uso di diagrammi al quadrato per mostrare visualmente l’area |
| Numeri quadrati perfetti | Elenchi e memorizzazione attraverso ripetizioni |
| Stima di radici non quadrate perfette | Confronto con i quadrati perfetti più vicini ed esercizi numerici |
Il metodo di approssimazione affina la comprensione degli studenti sulle proprietà delle radici quadrate. Gli studenti sono guidati a stimare valori di radici quadrate non esatte, come quella di 10, e a individuare, tra i numeri a loro conosciuti, il più vicino possibile al risultato reale.
Allo scopo di consolidare la padronanza degli argomenti, si assegnano tipicamente problemi che includono il calcolo di radici quadrate manualmente e con l’uso di calcolatrici. Si incoraggia l’uso di approcci logici e di capacità di stima attraverso compiti che mirano a riconoscere e risolvere problemi del mondo reale, dove questa operazione matematica trova applicazione. La progressione verso livelli più avanzati introduce radici quadrate di numeri non interi e il concetto di radicale, ampliando la conoscenza matematica dello studente.
