La misura dell’angolo tra due vettori in uno spazio vettoriale è definita attraverso il prodotto scalare tra i due vettori.

Il prodotto scalare di due vettori a e b, indicato con a·b, è dato dalla formula:

a·b = |a| |b| cos(θ)

Dove:

• |a| è la norma del vettore a
• |b| è la norma del vettore b
• cos(θ) è il coseno dell’angolo θ tra i vettori

L’angolo θ può essere calcolato usando la funzione arcocoseno (arccos), dato che:

θ = arccos(a·b / |a||b|)

Per vettori in uno spazio bidimensionale o tridimensionale, la misura dell’angolo è solitamente compresa tra 0° e 180°.

I passi per calcolare l’angolo tra due vettori sono:

1. Calcolare il prodotto scalare dei vettori.
2. Calcolare la norma di ciascun vettore.
3. Utilizzare la formula per l’arcocoseno per ottenere l’angolo.

Un angolo di 0° indica che i vettori sono paralleli e con la stessa direzione, mentre un angolo di 180° indica che sono paralleli ma con direzioni opposte. Un angolo di 90° mostra che i vettori sono perpendicolari tra loro.

Calcolo dell’angolo utilizzando il prodotto scalare

Il calcolo dell’angolo tra due vettori può essere eseguito impiegando il prodotto scalare, che fornisce una misura della loro direzione reciproca.

Introduzione al prodotto scalare

Il prodotto scalare, noto anche come prodotto interno o dot product, è un’operazione che associa a due vettori uno scalare. La definizione matematica è data dal prodotto delle magnitudini dei due vettori e dal coseno dell’angolo che formano tra loro.

• Formula generale del prodotto scalare:A ⋅ B = |A| |B| cos(θ)Dove A e B sono vettori, |A| e |B| rappresentano le loro magnitudini e θ è l’angolo tra i vettori.

Formula per il calcolo dell’angolo

L’angolo θ tra due vettori si può calcolare usando la formula inversa del coseno (arccos) e il prodotto scalare.

θ = arccos((A ⋅ B) / (|A| |B|))

La formula richiede la conoscenza previa delle magnitudini dei vettori e del loro prodotto scalare.

Esempi di calcolo

Per illustrare il concetto, consideriamo due vettori A = (a1, a2) e B = (b1, b2) nel piano cartesiano.

1. Calcolo del prodotto scalare:A ⋅ B = a1b1 + a2b2
2. Calcolo delle magnitudini:|A| = √(a1^2 + a2^2)|B| = √(b1^2 + b2^2)
3. Sostituzione nella formula dell’angolo:θ = arccos((a1b1 + a2b2) / (√(a1^2 + a2^2) √(b1^2 + b2^2)))Questo darà il valore dell’angolo θ in radianti, che può essere convertito in gradi se necessario.

Metodo del coseno dell’angolo

Il metodo del coseno dell’angolo è utilizzato nel calcolo dell’angolo tra due vettori in uno spazio bidimensionale o tridimensionale.

Definizione di coseno

Il coseno di un angolo in un triangolo rettangolo è definito come il rapporto tra il cateto adiacente all’angolo e l’ipotenusa. In termini più generali, il coseno è una funzione trigonometrica che descrive la relazione tra gli angoli e i lati di un triangolo qualsiasi.

Relazione tra coseno e angolo tra vettori

Nel contesto dei vettori, il coseno dell’angolo tra due vettori può essere calcolato utilizzando il prodotto scalare fra di essi e la norma (o lunghezza) dei vettori coinvolti. La formula è la seguente:

[ \cos(\theta) = \frac{\mathbf{v} \cdot \mathbf{w}}{|\mathbf{v}||\mathbf{w}|} ]

Dove:

• (\mathbf{v}) e (\mathbf{w}) sono i vettori in questione
• (\mathbf{v} \cdot \mathbf{w}) è il prodotto scalare tra i vettori
• (|\mathbf{v}|) e (|\mathbf{w}|) sono le norme dei vettori
• (\theta) è l’angolo tra i due vettori

Utilizzando questa relazione, è possibile determinare l’angolo preciso tra i due vettori attraverso il calcolo inverso del coseno, noto anche come arcocoseno.

Uso della funzione arccoseno per trovare l’angolo

Per determinare l’angolo tra due vettori nel piano o nello spazio, si può utilizzare la funzione arccoseno, indicata con “arccos”. La formula per il calcolo dell’angolo θ tra due vettori a e b è:

θ = arccos((a · b) / (|a| * |b|))

Dove “·” rappresenta il prodotto scalare tra i vettori e “|” indica la norma del vettore. Il prodotto scalare è dato dalla somma dei prodotti delle loro componenti corrispondenti:

a · b = a₁b₁ + a₂b₂ + … + aₙbₙ

Componente	Vettore a	Vettore b
1	a₁	b₁
2	a₂	b₂
…	…	…
n	aₙ	bₙ

La norma di un vettore, d’altra parte, è il modulo del vettore, che corrisponde alla radice quadrata della somma dei quadrati delle sue componenti. Viene così calcolata:

|a| = √(a₁² + a₂² + … + aₙ²)

Le operazioni devono essere eseguite nell’ordine matematico, prima il prodotto scalare, poi le norme dei vettori, e infine l’applicazione della funzione arccoseno al risultato della divisione tra il prodotto scalare e il prodotto delle norme.

Utilizzando questo metodo si può ottenere l’angolo θ in radianti; per convertirlo in gradi, moltiplicare per (180/π).

Questo approccio è basato su principi matematici solidi e non richiede l’uso di grafici o di misurazioni fisiche per trovare l’angolo.

Vettori in spazi bidimensionali

La comprensione dei vettori negli spazi bidimensionali è fondamentale per calcolare l’angolo tra due di essi utilizzando operazioni vettoriali standard.

Calcolo in R2

I vettori in uno spazio bidimensionale, noto come R2, sono definiti da due componenti: una x e una y.

Per calcolare l’angolo θ tra due vettori a = (a1, a2) e b = (b1, b2), si utilizza il prodotto scalare e la norma (o lunghezza) dei vettori.

Formula del Prodotto Scalare: [ \textbf{a} \cdot \textbf{b} = a1 \times b1 + a2 \times b2 ]

Norme dei Vettori: [ ||\textbf{a}|| = \sqrt{a1^2 + a2^2} ] [ ||\textbf{b}|| = \sqrt{b1^2 + b2^2} ]

Una volta ottenute queste quantità, l’angolo θ può essere determinato utilizzando la formula:

[ \cos(\theta) = \frac{\textbf{a} \cdot \textbf{b}}{||\textbf{a}|| \times ||\textbf{b}||} ]

Per ottenere l’angolo effettivo, si calcola l’arco coseno (arcos) del rapporto ottenuto.

Calcolare θ: [ \theta = \arccos\left(\frac{\textbf{a} \cdot \textbf{b}}{||\textbf{a}|| \times ||\textbf{b}||}\right) ]

I risultati vengono espressi in radianti o gradi, a seconda della preferenza o dei requisiti dell’applicazione specifica.

Vettori in spazi tridimensionali

Nell’ambito matematico, i vettori in spazi tridimensionali sono elementi fondamentali per la descrizione di oggetti e fenomeni nello spazio. Essi consistono di una tripla ordinata di numeri, rappresentanti le componenti lungo i tre assi cartesiani.

Calcolo in R3

Per calcolare l’angolo tra due vettori nello spazio tridimensionale ( \mathbb{R}^3 ), si utilizza la formula data dal prodotto scalare e la norma dei vettori.

Se ( \vec{a} ) e ( \vec{b} ) sono due vettori nello spazio, l’angolo ( \theta ) può essere determinato tramite l’equazione:

[ \cos(\theta) = \frac{\vec{a} \cdot \vec{b}}{| \vec{a} | | \vec{b} |} ]

dove:

• ( \vec{a} \cdot \vec{b} ) rappresenta il prodotto scalare definito da ( a_1b_1 + a_2b_2 + a_3b_3 )
• ( | \vec{a} | ) e ( | \vec{b} | ) sono le norme (o moduli) dei vettori, calcolate come ( \sqrt{a_1^2 + a_2^2 + a_3^2} ) e ( \sqrt{b_1^2 + b_2^2 + b_3^2} ) rispettivamente

Dal momento che il prodotto scalare misura la componente di un vettore nella direzione dell’altro, quando esso è pari a zero si deduce che i vettori sono ortogonali, ovvero l’angolo tra di loro è di 90 gradi. Il calcolo dell’angolo richiede il ricorso all’arcocoseno per ottenere il valore di ( \theta ) in radianti o gradi.

Norma dei vettori e sua importanza nel calcolo dell’angolo

La norma di un vettore, spesso indicata come ||v||, rappresenta la lunghezza o la grandezza del vettore in uno spazio euclideo. È fondamentale per misurare la distanza da l’origine al punto rappresentato dal vettore.

Per un vettore v con componenti (v1, v2, …, vn) in uno spazio n-dimensionale, la norma è definita come:

[ ||\textbf{v}|| = \sqrt{v_1^2 + v_2^2 + … + v_n^2} ]

In termini del calcolo dell’angolo tra due vettori, la norma gioca un ruolo cruciale—essa entra nella formula del prodotto scalare, strettamente collegato all’angolo.

Il prodotto scalare di due vettori a e b, denotato come a⋅b, è definito come:

[ \textbf{a} \cdot \textbf{b} = ||\textbf{a}|| \times ||\textbf{b}|| \times \cos(\theta) ]

dove θ rappresenta l’angolo tra i due vettori. Per trovare θ, si usa l’equazione:

[ \cos(\theta) = \frac{\textbf{a} \cdot \textbf{b}}{||\textbf{a}|| \times ||\textbf{b}||} ]

L’accuratezza nel calcolare la norma dei vettori è indispensabile per determinare l’angolo corretto. Un errore nella misurazione della norma di un vettore può portare a un risultato impreciso dell’angolo. Quindi, la norma dei vettori non è solo un concetto matematico astratto, ma una componente essenziale per applicazioni pratiche che richiedono misurazioni angolari precise, come nella robotica, fisica e grafica computerizzata.

Importanza dell’angolo tra vettori in fisica e ingegneria

L’angolo tra due vettori è un concetto fondamentale in diverse aree della fisica e dell’ingegneria. In fisica, la comprensione dell’angolo tra vettori permette di definire concetti come il lavoro, che è il prodotto scalare di forza e spostamento, e dipende dall’angolo tra i due vettori.

In ingegneria, gli angoli tra vettori sono essenziali per l’analisi delle strutture e la meccanica dei fluidi.

Per esempio, nel campo della dinamica dei fluidi, l’angolo tra il vettore velocità e il vettore superficie determina l’efficacia con cui un fluido esercita forza su una superficie.

Esempi di applicazioni comprendono:

• Dinamica: l’angolo tra vettori è usato nel calcolo della coppia e del momento angolare.
• Statistica: la misurazione dell’angolo tra vettori permette di valutare la correlazione tra variabili.

L’analisi degli angoli tra vettori utilizza spesso il teorema del coseno o la funzione arco coseno (arccos) per determinarli precisamente.

Problemi comuni nell’utilizzo delle formule e come risolverli

Quando si calcola l’angolo tra due vettori, è possibile incontrare difficoltà nell’applicazione delle formule. Una corretta comprensione dei passaggi può ridurre significativamente gli errori.

Errore di calcolo del prodotto scalare: Quando si moltiplicano i componenti dei vettori, un errore comune è la somma scorretta dei prodotti. È essenziale eseguire i calcoli con attenzione.

Soluzione: Utilizzare la formula del prodotto scalare [ a \cdot b = a_xb_x + a_yb_y + a_zb_z ].

Imprecisione nel calcolo della norma: La norma di un vettore determina la sua lunghezza e richiede l’applicazione della radice quadrata della somma dei quadrati dei suoi componenti.

Soluzione: Impiegare correttamente la formula della norma [ ||a|| = \sqrt{a_x^2 + a_y^2 + a_z^2} ].

Difficoltà nella formula dell’angolo: L’angolo tra due vettori è calcolato utilizzando l’arcocoseno del rapporto tra il prodotto scalare e il prodotto delle norme dei due vettori.

Soluzione: Applicare la formula [ \theta = \arccos\left(\frac{a \cdot b}{||a|| \times ||b||}\right) ]

Mancata normalizzazione dei vettori: Il calcolo può risultare più semplice se i vettori sono normalizzati, ovvero ridotti a una norma unitaria.

Soluzione: Normalizzare i vettori prima di inserirli nella formula dell’angolo.

Errore nel range dell’arcocoseno: Il valore restituito dall’arcocoseno può variare tra 0 e π radianti, o tra 0 e 180 gradi. Assicurarsi che la calcolatrice o il software utilizzato siano impostati correttamente.

Soluzione: Verificare l’impostazione della calcolatrice su radianti o gradi a seconda dell’esigenza.

Applicazioni pratiche del calcolo dell’angolo tra vettori

Nel mondo della fisica, il calcolo dell’angolo tra vettori è cruciale per comprendere le forze che agiscono sugli oggetti.

Per esempio, l’angolo di attrito viene utilizzato per determinare la forza necessaria per muovere un oggetto lungo una superficie.

Nell’ingegneria meccanica, questo calcolo aiuta nella progettazione di componenti che devono assorbire o trasmettere forze lungo direzioni specifiche.

I robot manipolatori, che necessitano di precisione nel posizionamento degli arti, utilizzano questi calcoli per ottimizzare il movimento e ridurre l’usura meccanica.

In ambito informatico, il calcolo è fondamentale nello sviluppo di grafica computerizzata e videogiochi.

A titolo di esempio, la determinazione dell’angolo tra vettori è essenziale per calcolare l’illuminazione, le ombre e le collisioni tra oggetti in uno spazio tridimensionale.

In campo economico e finanziario, il calcolo dell’angolo tra due serie di dati può significare la correlazione tra due variabili economiche. Un angolo vicino a zero indica una forte correlazione positiva, mentre un angolo di circa 180 gradi indica una forte correlazione negativa.

La navigazione e la localizzazione satellitare fanno un uso intensivo di questo calcolo per determinare la posizione e l’orientamento degli oggetti sulla Terra o nello spazio.

In geologia, lo studio della direzione e dell’angolazione delle formazioni rocciose può fornire preziose informazioni sulle forze tettoniche e sull’ambiente di deposizione.

Strumenti software e calcolatrici online per l’angolo tra vettori

Nell’ambito matematico, diversi strumenti software e calcolatrici online sono disponibili per calcolare l’angolo tra due vettori.

Questi strumenti utilizzano formule della geometria analitica per determinare la misura angolare basandosi sul prodotto scalare e la norma dei vettori.

• GeoGebra: Un’applicazione interattiva che permette calcoli vettoriali e di visualizzare graficamente i vettori nel piano o nello spazio. Utilizza un’interfaccia intuitiva per inserire i vettori e fornisce istantaneamente il rispettivo angolo.
• Wolfram Alpha: Questo motore di calcolo computazionale fornisce risultati precisi per il calcolo dell’angolo tra due vettori. Inserendo le coordinate dei vettori, l’utente riceve una valutazione dettagliata dell’angolo, incluso il processo di calcolo.

Strumento	Caratteristiche	URL
GeoGebra	Grafici interattivi, facile da usare	https://www.geogebra.org/
Wolfram Alpha	Risultati analitici dettagliati	https://www.wolframalpha.com/

Questi strumenti sono particolarmente utili per studenti, ingegneri e professionisti nel campo scientifico che richiedono calcoli precisi per i loro progetti e ricerche. La facilità di utilizzo e l’accessibilità attraverso piattaforme online permettono a chiunque di applicare questi concetti matematici senza la necessità di un software dedicato.

Confronto tra metodi analitico e numerico nel calcolo dell’angolo

Il calcolo dell’angolo tra due vettori può essere effettuato attraverso metodi analitici o numerici.

Il metodo analitico utilizza la formula basata sul prodotto scalare dei vettori e sulla norma dei vettori coinvolti.

Formula Analitica: 

   

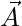dove:

• e 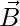sono i vettori
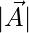• indica il prodotto scalare
• e 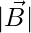sono le norme dei vettori

I metodi numerici, invece, approssimano l’angolo utilizzando algoritmi iterativi che possono essere implementati su computer.

L’approccio numerico è spesso impiegato per i calcoli su vettori in spazi con dimensioni elevate o quando i dati subiscono delle fluttuazioni dovute all’errore di misurazione o di arrotondamento.

Confronto:

Criterio	Metodo Analitico	Metodo Numerico
Precisione	Alta, esatta se non ci sono errori di arrotondamento	Variabile, dipende dall’algoritmo e dalla precisione del calcolo numerico
Complessità	Basso, formule dirette	Variabile, a seconda dell’algoritmo
Applicabilità	Ampia su vettori in R² e R³	Preferibile in spazi di dimensione superiore o con dati incerti

Mentre il metodo analitico è accurato e diretto per vettori in spazi bi e tridimensionali, il metodo numerico fornisce una flessibilità di calcolo in contesti dove i dati possono essere soggetti a variazioni o gli spazi vettoriali sono di dimensione elevata.

Immagine in evidenza: www.andreaminini.org