La deviazione standard è uno degli indicatori statistici più impiegati in quanto offre una preziosa misura della dispersione dei dati, il che è fondamentale in numerose discipline scientifiche, economiche e sociali.

Oltre che ad offrire un utile (speriamo) calcolatore della deviazione standard per un campione, il presente articolo si propone di esplorare in modo approfondito la deviazione standard, illustrando non solo il suo calcolo ma anche le sue applicazioni pratiche in vari contesti.

Verranno discusse le formule fondamentali per la popolazione e i campioni, accompagnate da esempi pratici che dimostrano come queste misurazioni possano essere applicate per interpretare dati reali.

Inoltre, verrà evidenziato l’uso di software e strumenti digitali per il calcolo della deviazione standard, facilitando così compiti analitici complessi e migliorando l’accuratezza delle interpretazioni.

L’obiettivo è fornire una guida chiara e dettagliata che possa servire da riferimento sia per gli studenti che per i professionisti, aiutando a comprendere meglio come la deviazione standard possa essere utilizzata per fare inferenze più precise su insiemi di dati.

Definizione

La deviazione standard, spesso indicata con il simbolo σ (sigma), è un indicatore statistico fondamentale per misurare la dispersione dei dati rispetto alla loro media (Lindgren, 1993).

Un valore basso di deviazione standard indica che i dati sono concentrati intorno alla media, mentre un valore elevato suggerisce una maggiore dispersione.

Per calcolare la deviazione standard, si seguono diversi passaggi, tra cui il calcolo della media, la determinazione degli scarti dalla media, l’elevamento al quadrato di tali scarti e infine il calcolo della radice quadrata della loro media.

Questa è la formula della dispersione per una popolazione completa:

σ = √(Σ(x – μ)² / N)

Dove σ è la deviazione standard, x rappresenta ciascun valore dei dati, μ è la media dei dati e N è il numero totale dei dati.

Per un campione preso da una popolazione, la formula si modifica leggermente:

s = √(Σ(x – m)² / (n – 1))

Qui, s è la deviazione standard del campione, m è la media del campione e n è il numero di osservazioni nel campione.

L’uso di questa misura di dispersione fornisce un’indicazione di quanto i valori del set si discostano dalla media.

Valori piccoli indicano che i dati sono raggruppati vicini alla media, mentre valori maggiori suggeriscono una maggiore dispersione dei dati.

Calcolatore deviazione standard di una popolazione

Inserisci i numeri separati da uno spazio (es. “1 2 3 4”) o da uno spazio e una virgola (es. “1, 2, 3, 4”). Come separatore per le cifre decimali utilizza il punto (es. “10.1”) e non la virgola (es. “10,1)

Risultato

Somma:

Media aritmetica:

Deviazione standard:

Calcolo della deviazione standard per un campione

In statistica la deviazione standard per un campione misura quanto i valori si diffondono rispetto alla media del campione.

Formula per il campione

La formula per calcolare la deviazione standard $s$ di un campione è la seguente:

$s = √(Σ(x - x̄)² / (n-1))$

dove $x_i$ rappresenta ciascun valore nel campione, $\overline{x}$ è la media campionaria dei valori e $n$ è il numero di osservazioni nel campione. La differenza tra $n$ e 1 nel denominatore tiene conto della correzione per la stima di un campione.

Passaggi calcolo manuale

I passaggi per il calcolo manuale di un campione sono:

Calcolare la media 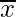$\overline{x}$ del campione sommando tutti i valori e dividendo per il numero di osservazioni.
Sottrarre la media campionaria da ogni valore del campione per ottenere le differenze.
Elevare al quadrato ciascuna differenza.
Sommare tutti i quadrati delle differenze.
Dividere la somma ottenuta per 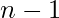$n-1$ , dove 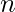$n$ è il numero totale di valori.
Calcolare la radice quadrata del risultato.

Esempio con dati reali

Si consideri il seguente campione di dati: 5, 7, 9, 4, 6. Si procede al calcolo per il campione:

La media 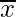$\overline{x}$ è $(5+7+9+4+6)/5 = 6.2$ .
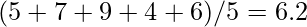Le differenze dalla media sono: $-1.2, 0.8, 2.8, -2.2, -0.2$ .
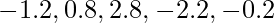I quadrati delle differenze sono: $1.44, 0.64, 7.84, 4.84, 0.04$ .
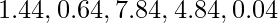La somma dei quadrati è $1.44 + 0.64 + 7.84 + 4.84 + 0.04 = 14.8$ .
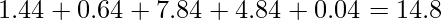Dividendo per 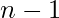$n-1$ , ovvero per 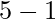$5-1$ , si ottiene $14.8/4 = 3.7$ .
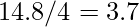La radice quadrata di 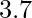$3.7$ dà $\sqrt{3.7} \approx 1.92$ .

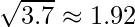Quindi, la deviazione standard per questo campione di dati è circa 1.92.

Calcolo della deviazione standard per una popolazione

La deviazione standard di una popolazione è una misura statistica che indica quanto i dati si diffondono rispetto alla media (valore medio) della popolazione.

Formula per la Popolazione

La formula per calcolare la deviazione standard $σ$ per una popolazione intera è:

σ = √[Σ(xi – μ)² / N]

dove:

σ rappresenta la deviazione standard della popolazione
xi indica ciascun valore nella popolazione
μ è la media (o valore atteso) della popolazione
N è il numero totale di valori nella popolazione
√ simboleggia la radice quadrata
Σ denota la sommatoria di tutte le differenze al quadrato tra ogni valore e la media

Per calcolare la deviazione standard si eleva al quadrato la differenza tra ogni valore della popolazione e la media, si sommano tutte queste differenze al quadrato, si divide il risultato per il numero totale dei valori (N) e infine si calcola la radice quadrata del quoziente.

Differenze rispetto al campione

Quando si calcola la deviazione standard per un campione di una popolazione anziché per l’intera popolazione, si utilizza una formula leggermente diversa da quella della deviazione standard della popolazione.

La formula per il campione sostituisce N con N-1, dove N è il numero di osservazioni nel campione. Questo metodo si chiama “correzione di Bessel” ed è necessario perché la stima deve tenere conto che si sta lavorando con un sottoinsieme della popolazione, il che introduce un livello di incertezza.

La formula per il campione è:

s = √[Σ(xi – x̄)² / (n – 1)]

dove:

s è la deviazione standard del campione
xi rappresenta ciascun valore nel campione
x̄ è la media campionaria
n è il numero di osservazioni nel campione

La differenza principale è, quindi, nel divisore della sommatoria: si usa N per la popolazione e N-1 per il campione. Questa modifica garantisce una stima non distorta della misura della popolazione sulla base di un campione.

Strumenti software per il calcolo

I metodi per calcolare questa misura sono molteplici e si avvalgono spesso di strumenti software. Tali applicativi offrono precisione e velocità, facilitando l’analisi statistica.

Utilizzo del foglio di calcolo

Il foglio di calcolo è uno strumento versatile nell’ambito dell’elaborazione dati. Programmi come Microsoft Excel o Google Sheets forniscono funzioni integrate per il calcolo della deviazione standard. Esempi di queste funzioni includono:

STDEV.P() (Deviazione standard della popolazione)
STDEV.S() (Deviazione standard del campione)

Si applicano seguendo la sintassi:

=STDEV.P(intervallo di dati)
=STDEV.S(intervallo di dati)

L’utente deve semplicemente inserire l’intervallo di celle contenenti i dati per ottenere il valore cercato.

Software statistico

Software specializzati come SPSS, SAS o R forniscono strumenti più avanzati per il calcolo della dispersione, adatti a ricerche complesse. Questi programmi includono comandi dedicati, tra cui:

sd() in R
PROC MEANS in SAS
‘Analyze -> Descriptive Statistics -> Descriptives’ in SPSS

Questi comandi permettono di calcolare la nostra misura insieme ad altre statistiche descrittive, offrendo un’analisi dettagliata dei dati.

Teoria statistica di base

In questa sezione esploreremo la varianza e la distribuzione normale, due concetti fondamentali nella statistica .

La varianza

La varianza è una misura della dispersione dei valori in un insieme di dati rispetto alla media. Si calcola elevando al quadrato la differenza fra ciascun valore e la media aritmetica e sommando i risultati ottenuti. Questo valore sommato viene poi diviso per il numero di osservazioni meno uno, che rappresenta i gradi di libertà. La formula è la seguente:

$\text{Varianza} (s^2) = \frac{\sum_{i=1}^{n} (x_i - \bar{x})^2}{n-1}$

dove:

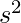$s^2$ rappresenta la varianza campionaria,
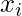$x_i$ è il singolo valore osservato,
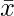$\bar{x}$ è la media aritmetica dei valori osservati,
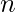$n$ è il numero totale di osservazioni.

Distribuzione normale e standardizzazione

La distribuzione normale, anche chiamata Gaussiana, è una delle distribuzioni probabilistiche più importanti in statistica.

La sua funzione di densità ha la forma di una campana simmetrica, definita dai parametri media $\mu$ e deviazione standard $\sigma$ .

La standardizzazione è un processo che trasforma una distribuzione qualunque in una distribuzione normale standard con media 0 e deviazione standard 1.

Si effettua sottraendo la media da ciascun valore dell’insieme di dati e dividendo il risultato per la deviazione standard:

$z = \frac{x - \mu}{\sigma}$

Questo rende possibile confrontare valori provenienti da diverse distribuzioni normali.

Applicazioni pratiche

La misura della dev. std. quantifica la dispersione dei dati rispetto alla media. È utilizzata in una serie di contesti per comprendere la variabilità e gli schemi all’interno di un set di dati.

Analisi dei dati

Nell’analisi dei dati fornisce una valutazione immediata della variabilità di un insieme di misure.

È essenziale nel confrontare la consistenza di due serie di dati.

Per esempio, in uno studio sulla pressione sanguigna, la deviazione standard può facilitare la comprensione della consistenza delle misurazioni all’interno di un gruppo di individui.

Media della pressione sanguigna: 120 mmHg
Deviazione standard: 15 mmHg

In questo caso, i valori di pressione sanguigna possono differire in media di 15 mmHg dalla media.

Controllo di qualità

Nel controllo di qualità, la misura serve invece a monitorare la consistenza di un processo produttivo.

Un basso valore indica che il processo è sotto controllo e produce articoli omogenei.

Ad esempio, in un processo di fabbricazione di componenti elettronici, la deviazione standard può indicare la precisione delle dimensioni prodotte.

Componente	Dimensioni nominali	Deviazione Standard
Resistenze	2 mm	0.02 mm
Condensatori	5 mm	0.01 mm

Qui vediamo che le dimensioni delle resistenze mostrano una variazione di 0.02 mm dalla dimensione nominale, suggerendo un controllo di qualità elevato nel processo produttivo.

Interpretazione

La deviazione standard offre un metodo quantitativo per valutare la variabilità in un insieme di dati.

Quando il valore della deviazione standard è piccolo, i dati sono generalmente raggruppati vicino alla media, indicando una bassa variabilità.

Al contrario, un valore elevato suggerisce una maggiore diffusione dei dati e quindi una variabilità più alta.

Poi la deviazione standard permette di distinguere tra campioni con alta e bassa variabilità:

Alta Variabilità: I valori sono molto differenti l’uno dall’altro e distanti dalla media.
Bassa Variabilità: I valori sono simili tra loro e vicini al valore medio.

La distinzione è fondamentale per interpretare correttamente i set di dati, poiché influisce sull’affidabilità delle stime medie e sulla generalizzazione dei risultati ad un’intera popolazione.

Limitazioni di questa misura

La dev. std. è un indice di dispersione molto usato, ma presenta delle limitazioni nel suo utilizzo che ne condizionano l’efficacia.

Dati non normali

La deviazione standard assume che i dati siano distribuiti normalmente. Tuttavia, in presenza di una distribuzione non normale, questo parametro può non fornire un’indicazione accurata dell’effettiva variabilità dei dati.

Distribuzione non normale: Le distribuzioni asimmetriche sono un esempio di set di dati per cui la deviazione standard può risultare fuorviante.

Outlier e impatto

La presenza di outlier, ovvero di valori molto distanti dalla media, può distorcere la deviazione standard, amplificando la percezione della dispersione dei dati.

Outlier: Alti o bassi estremi influiscono significativamente sulla deviazione standard.
Impatto: La deviazione standard risulta più grande con outlier, che potrebbe non riflettere la variabilità della maggior parte dei dati.

Confronto tra deviazione standard e varianza

La deviazione standard e la varianza sono entrambe misure di dispersione statistiche, usate per quantificare la variabilità o la dispersione dei dati in un set.

Mentre la prima esprime la dispersione in unità originali dei dati, la varianza rappresenta la dispersione in termini di quadrati di tali unità.

Differenze concettuali

La deviazione standard, denotata come σ (sigma), è la radice quadrata della varianza. Offre una stima della dispersione dei valori di un insieme di dati rispetto alla loro media.

La formula per calcolarla è

$σ = \sqrt{ \frac{1}{N} \sum_{i=1}^{N}(x_i - μ)^2 }$

dove $(x_i)$ rappresentano i valori dei dati, $(μ)$ è la media aritmetica, e $(N)$ è il numero totale di osservazioni.

La varianza, simboleggiata con $(σ^2)$ , è il quadrato della deviazione standard e si focalizza sul grado di variabilità dei dati.

La sua formula è

$σ^2 = \frac{1}{N} \sum_{i=1}^{N}(x_i - μ)^2$

In altre parole, la deviazione standard è un indice più direttamente confrontabile con i dati originali, mentre la varianza, essendo il quadrato degli scarti dalla media, fornisce una misura che esagera i contributi dei valori più distanti dalla media.

Scelta della misura più adatta

La scelta se utilizzare la deviazione standard o la varianza dipende dall’obiettivo dell’analisi statistica.

Deviazione Standard:
- Si presta bene quando si desidera descrivere la dispersione in termini simili ai dati originali.
- È più intuitiva e facilmente interpretabile, soprattutto per la comunicazione dei risultati a un pubblico non specializzato.
Varianza:
- Utile in contesti analitici più complessi, come nelle operazioni algebriche che coinvolgono le distribuzioni di probabilità.
- Viene spesso impiegata nelle analisi statistiche avanzate, come quelle che coinvolgono variabili casuali e attese matematiche.

Deviazione standard normalizzata

Questa è una misura che permette di confrontare la dispersione di insiemi di dati con differenti unità di misura o varie medie.

Essa utilizza il coefficiente di variazione e la standardizzazione dei valori per normalizzare i dati.

Coefficiente di variazione

Il coefficiente di variazione $CV$ è il rapporto tra la deviazione standard $σ$ e la media $μ$ del set di dati, solitamente espresso in percentuale.

La formula per calcolare il CV è la seguente:

$CV = \Bigl(\frac{σ}{μ}\Bigr) \times 100 %$

Per esempio, in un insieme di dati con una media di 50 e una deviazione standard di 5, il coefficiente di variazione è:

$CV = \Bigl(\frac{5}{50}\Bigr) \times 100 % = 10%$

Questo indice è particolarmente utile per confrontare la variabilità relativa tra serie di dati diverse.

Standardizzazione dei valori

La standardizzazione dei valori implica la conversione di punteggi originali in una scala comune che ha una media di zero e una deviazione standard di uno.

Tale processo è conosciuto anche come punteggio z ed è calcolato attraverso la formula:

$z = \frac{(X - μ)}{σ}$

Dove X rappresenta il valore originale, μ è la media e σ la deviazione standard dei dati.

Se un dato ha un punteggio z di -2, significa che è due deviazioni standard al di sotto della media del set di dati.

La standardizzazione è essenziale per confrontare valori provenienti da distribuzioni diverse.

Errore di stima

L’errore di stima si verifica quando i dati vengono manipolati in maniera errata durante il calcolo della deviazione standard. Questo può accadere in diversi modi:

Uso errato della formula: Esistono due formule per calcolare la deviazione standard. Una è per i campioni (s) e l’altra per l’intera popolazione (σ). Usare la formula sbagliata può portare a risultati inaccurati. Formula per la deviazione standard di un campione (s)Formula per la deviazione standard di una popolazione (σ) $\sqrt{\frac{1}{n-1}\sum_{i=1}^{n}(x_{i}-\bar{x})^{2}}$ $\sqrt{\frac{1}{N}\sum_{i=1}^{N}(X_{i}-\mu)^{2}}$

Trattamento scorretto dei dati mancanti: Omettere o sostituire in modo inappropriato i dati mancanti può alterare significativamente la deviazione standard.

Applicazioni “reali” di questa misura di dispersione

Nel campo della finanza, la deviazione standard è ampiamente utilizzata per misurare la volatilità dei prezzi degli asset finanziari. Uno studio condotto da Markowitz (1952) ha dimostrato che la deviazione standard è un indicatore chiave per valutare il rischio associato a un determinato investimento. Ad esempio, un fondo d’investimento con una deviazione standard elevata rispetto al rendimento medio suggerisce una maggiore volatilità, indicando un rischio più alto e potenzialmente rendimenti più elevati o perdite.

In medicina, la deviazione standard aiuta a comprendere la variabilità nelle risposte dei pazienti a un trattamento. Per esempio, nello studio della pressione sanguigna, una deviazione standard bassa in un gruppo di pazienti trattati con un nuovo farmaco può indicare che il farmaco ha un effetto uniforme sulla riduzione della pressione sanguigna. Al contrario, una deviazione standard alta potrebbe suggerire una risposta variabile, richiedendo ulteriori indagini per determinare i fattori che influenzano tali variazioni.

Nell’ingegneria, in particolare nel controllo di qualità e nei processi produttivi, la deviazione standard è fondamentale per monitorare la consistenza e l’affidabilità di prodotti e componenti. Ad esempio, in un processo di produzione, una deviazione standard ridotta nelle dimensioni dei componenti assemblati indica un alto grado di precisione e uniformità, essenziale per garantire la qualità e la funzionalità del prodotto finale.

Prestazioni Sportive: anche per gli sportivi la deviazione standard offre spunti importanti. Consideriamo, ad esempio, un allenatore che analizza i tempi di giro di un nuotatore durante gli allenamenti. Una bassa deviazione standard nei tempi di giro indica una prestazione consistente, mentre una deviazione standard alta potrebbe suggerire la necessità di migliorare l’equilibrio e la stamina dell’atleta. Un allenatore di nuoto ha detto: “Monitoriamo la deviazione standard dei tempi di giro per valutare la consistenza dell’atleta”. Questo ci aiuta a personalizzare gli allenamenti per migliorare le loro performance in modo mirato

Questi semplici esempi sono la prova che comprendere e applicare correttamente la deviazione standard non solo arricchisce l’analisi statistica ma consente anche di navigare con maggiore sicurezza attraverso la complessità dei dati, migliorando così la qualità delle decisioni basate su questi ultimi.

Riferimenti bibliografi e risorse

Tra i testi (in inglese) fondamentali per comprendere deviazione standard menzioniamo:

B. W. Lindgren, “Statistical Theory” (Quarta edizione, Chapman & Hall) Il volume offre una trattazione approfondita delle basi teoriche della statistica, con particolare attenzione alle misure di variabilità come la deviazione standard.
D. J. Hand, et al., “Handbook of Small Data Sets” (Chapman & Hall) Questo testo include una vasta gamma di set di dati utilizzabili per esercitarsi nel calcolo della deviazione standard, oltre a fornire esempi pratici sull’impiego di tali misure in vari ambiti di ricerca.
Standard Deviation in Trading: Calculations, Use Cases, Examples and more. (2024, March 7). Quantitative Finance & Algo Trading Blog by QuantInsti. https://blog.quantinsti.com/standard-deviation/
The Money Alert. (2024, April 12). What is Standard Deviation? Understanding its Role in Accessing Risk. The Money Alert. https://themoneyalert.com/what-is-standard-deviation/
Meagher, P. (2023, January 9). Std Deviation In Finance: Applications & Examples. Learnsignal. https://www.learnsignal.com/blog/standard-deviation-finance-applications-examples/

Risorse online (in inglese):

Statsoft, “Electronic Statistics Textbook” Un testo di statistica completo è disponibile online. Include una sezione dedicata alla deviazione standard. Questa sezione ha definizioni chiare e esempi pratici. Puoi trovarlo al seguente link: Statsoft Textbook
Khan Academy, “Standard Deviation” Una piattaforma di apprendimento offre lezioni e video tutorial su una vasta gamma di argomenti statistici. Tra questi, troverai la deviazione standard. Ogni lezione include esempi e quiz per rinforzare la comprensione dell’argomento. Puoi accedervi all’indirizzo: Khan Academy Statistics

Calcolatore deviazione standard

Definizione

Calcolatore deviazione standard di una popolazione

Risultato

Calcolo della deviazione standard per un campione

Formula per il campione

Passaggi calcolo manuale

Esempio con dati reali

Calcolo della deviazione standard per una popolazione

Formula per la Popolazione

Differenze rispetto al campione

Strumenti software per il calcolo

Utilizzo del foglio di calcolo

Software statistico

Teoria statistica di base

La varianza

Distribuzione normale e standardizzazione

Applicazioni pratiche

Analisi dei dati

Controllo di qualità

Interpretazione

Limitazioni di questa misura

Dati non normali

Outlier e impatto

Confronto tra deviazione standard e varianza

Differenze concettuali

Scelta della misura più adatta

Deviazione standard normalizzata

Coefficiente di variazione

Standardizzazione dei valori

Errore di stima

Applicazioni “reali” di questa misura di dispersione

Riferimenti bibliografi e risorse

Leave a Reply Cancel Reply

CALCOLO.ONLINE