Media ponderata:
La media ponderata è un tipo di media che tiene conto dell’importanza (o peso) di ciascun valore. Invece di fare semplicemente la somma dei valori divisa per il numero totale (come nella media aritmetica), si moltiplica ogni valore per un peso e poi si divide la somma dei prodotti per la somma dei pesi.
Per esprimere tale calcolo si applica la formula:
![]()
Dove valore ![]() rappresenta il numero di cui si calcola la media e peso
rappresenta il numero di cui si calcola la media e peso ![]() indica il peso assegnato a quel specifico valore. Il risultato è la somma dei prodotti di ciascun valore per il suo peso, divisa per la somma dei pesi.
indica il peso assegnato a quel specifico valore. Il risultato è la somma dei prodotti di ciascun valore per il suo peso, divisa per la somma dei pesi.
In un contesto online, le piattaforme per il calcolo della media ponderata permettono agli utenti di inserire i valori e i relativi pesi attraverso un’interfaccia digitale, ottenendo immediatamente il risultato desiderato. Questi strumenti sono particolarmente utili per studenti e professionisti che necessitano di calcoli rapidi e precisi senza doverli effettuare manualmente.
Esempio di applicazione:
| Valore (nota) | Peso (crediti) |
|---|---|
| 28 | 6 |
| 30 | 12 |
| 24 | 3 |
Utilizzando i dati sopra, la media ponderata si calcolerebbe sommando i prodotti delle note per i crediti (totale ponderato) e dividendo il risultato per la somma dei crediti, fornendo così una media che tiene conto dell’importanza di ogni singolo esame basato sui crediti corrispondenti.
Applicazioni Pratiche
La media ponderata online si rivela uno strumento cruciale in diverse applicazioni. Il suo utilizzo in campo educativo e nelle recensioni permette una valutazione più equa e rappresentativa.
Istruzione e Formazione
Nell’ambito educativo, la media ponderata è impiegata per calcolare il punteggio finale degli studenti. Ogni valutazione ha un ‘peso’ diverso in base alla sua importanza relativa all’interno del curriculum. Per esempio:
| Valutazione | Peso | Voto |
|---|---|---|
| Test intermedio | 30% | 24/30 |
| Progetto | 50% | 27/30 |
| Partecipazione | 20% | 18/20 |
La media ponderata si ottiene moltiplicando ogni voto per il suo peso e sommando il risultato, poi diviso per la somma dei pesi.
Recensioni e Valutazioni Online
Nella valutazione di prodotti o servizi online, le recensioni sono spesso aggregate in una media ponderata. I giudizi degli utenti vengono ponderati in funzione di vari fattori, come la recentità della recensione e la verifica dell’acquisto. Ciò assicura che il feedback più pertinente e affidabile riceva un’influenza maggiore nella valutazione complessiva. Ad esempio:
| Recensione | Fattore di ponderazione | Voto (su 5) |
|---|---|---|
| Acquisto verificato, 1 mese fa | 2.0 | 4 |
| Acquisto non verificato, 6 mesi fa | 1.0 | 5 |
| Acquisto verificato, 1 anno fa | 0.5 | 3 |
La media ponderata delle recensioni è calcolata tenendo conto di questi fattori, offrendo quindi una rappresentazione più accurata della soddisfazione del cliente.
Strumenti per il calcolo della media ponderata
Il calcolo della media ponderata è un’operazione matematica che attribuisce diversi pesi ai valori di un set di numeri. Questo principio si trova spesso applicato nel campo dell’educazione per calcolare la media dei voti degli studenti tenendo conto del peso di ciascun esame. Numerosi strumenti online permettono di eseguire questo calcolo automaticamente.
Calcolatori Online: Diversi siti web offrono calcolatori di media ponderata che richiedono l’input dei voti e dei loro rispettivi pesi. Questi strumenti generano rapidamente la media ponderata.
- Esempio di siti popolari per il calcolo:
- Mediaponderata.it
- Calcolomedie.it
Fogli di calcolo: Piattaforme come Microsoft Excel e Google Sheets permettono agli utenti di creare formule personalizzate per il calcolo della media ponderata.
| Fase | Azione |
|---|---|
| 1 | Inserire i voti in una colonna |
| 2 | Inserire i pesi corrispondenti in un’altra colonna |
| 3 | Utilizzare la formula dedicata per calcolare la media |
Applicazioni Mobile: Disponibili su iOS e Android, molte app forniscono funzioni simili ai siti web, con l’aggiunta della portabilità.
Nota bene: È fondamentale inserire i dati correttamente per garantire l’accuratezza del risultato. Gli strumenti sopra citati non sostituiscono il controllo umano, che rimane essenziale per verificarne l’attendibilità.
Metodologia di Ponderazione
La ponderazione nei media online è una metodica che attribuisce differenti pesi ai contenuti in base a criteri predefiniti, per riflettere l’importanza relativa di ciascun elemento analizzato.
Pesi Variabili
La scelta dei pesi variabili si basa sull’assunto che non tutti i contenuti mediatici rivestano lo stesso grado di importanza o rilevanza. Per stabilire il peso di un contenuto, si analizzano variabili quali l’attinenza al pubblico, l’autorevolezza delle fonti e il potenziale impatto del messaggio veicolato. Queste variabili possono essere rappresentate come segue:
| Variabile | Descrizione |
|---|---|
| Attinenza al pubblico | Grado di interesse che il contenuto suscita nel pubblico di riferimento. |
| Autorevolezza delle fonti | Livello di affidabilità e competenza delle fonti citate. |
| Impatto del messaggio | Estensione dell’effetto che il contenuto ha sull’audience. |
La combinazione ponderata di questi elementi determina il valore complessivo attribuito a ogni contenuto.
Scelta dei Pesi
La scelta dei pesi è un processo cruciale che richiede l’applicazione di metodologie statistiche e di analisi dei dati. Viene spesso affidata a team di esperti che considerano numerosi fattori, tra cui le metriche di engagement (come visualizzazioni
, condivisioni, commenti), la frequenza di pubblicazione e la pertinenza temporale.
Per esempio:
- Engagement:
- Visualizzazioni: 30%
- Condivisioni: 20%
- Commenti: 15%
- Frequenza di pubblicazione: 25%
- Pertinenza temporale: 10%
Questa distribuzione dei pesi serve a garantire che i risultati della ponderazione siano equilibrati e rappresentativi dell’impatto di ogni contenuto nell’ambiente mediatico.
Vantaggi dell’uso di media ponderata online
L’uso di media ponderata online offre numerosi vantaggi in varie applicazioni. La media ponderata è un calcolo matematico che assegna pesi diversi a diversi elementi, fornendo un valore che riflette l’importanza relativa di ciascuno.
- Accessibilità: Strumenti online consentono un facile accesso ai calcoli di media ponderata, disponibili a studenti e professionisti.
- Precisione: Le piattaforme online sono progettate per garantire alta precisione nei calcoli, riducendo il rischio di errori umani.
Velocità ed Efficienza: Il calcolo manuale di medie ponderate richiede tempo. Piattaforme online eseguono il calcolo quasi istantaneamente, migliorando l’efficienza del processo.
- Funzioni Aggiuntive: Offrono funzioni come la conservazione dei dati per uso futuro e grafici integrati, utili per analizzare i risultati.
Risorse Educative: Molti siti incorporano risorse didattiche che aiutano nell’interpretazione dei risultati, favorendo l’apprendimento degli utenti.
- Costo:
- Economicità: Molte applicazioni per calcolare la media ponderata online sono gratuite o hanno costi limitati.
- Riduzione di spese per materiali didattici: Minimizzano la necessità di acquistare manuali o strumenti fisici.
Utilizzare media ponderata online facilita la gestione delle priorità in contesti educativi e professionali, fornendo un mezzo efficace per valutare l’impatto di svariati fattori in situazioni analitiche.
Obiettivi futuri e limitazioni
Nel panorama dell’analisi media ponderata online, esistono diverse sfide e limitazioni che impattano la raccolta e l’interpretazione dei dati. La varianza qualitativa dei dati può essere un fattore critico: non tutte le fonti online forniscono informazioni di qualità paragonabile, portando a possibili distorsioni nell’analisi.
Una seconda sfida è rappresentata dalla selettività dell’accesso ai dati. Molte piattaforme limitano l’accesso alle informazioni per proteggere la privacy degli utenti o per politiche interne, il che può ostacolare un’analisi completa.
L’ambiguità semantica è un altro ostacolo significativo. Nell’interpretare i dati, le sfumature linguistiche o il contesto possono alterare il significato, soprattutto quando si analizzano dati testuali come i post sui social media.
| Sfida | Descrizione |
|---|---|
| Varianza qualitativa | Differenze nella qualità delle fonti |
| Accesso ai dati | Limitazioni all’accesso imposte dalle piattaforme |
| Ambiguità semantica | Complessità nella comprensione del contesto e del linguaggio |
Inoltre, la rapida evoluzione del panorama digitale comporta continui aggiornamenti delle piattaforme e dei relativi algoritmi, rendendo arduo mantenere metodi di analisi costantemente aggiornati. L’applicabilità delle analisi è spesso circoscritta dal cambio di tendenze e tecnologie.
La rappresentatività dei dati online può anche portare a sfide statistiche. Non tutti gli strati sociali sono rappresentati equamente online, il che può generare bias nelle conclusioni di uno studio.
Questi ostacoli richiedono attenzioni particolari nella progettazione e nell’implementazione di metodiche di analisi media ponderata, al fine di garantire risultati affidabili.
Elementi di statistica necessari
Per comprendere il concetto di media ponderata online, è essenziale acquisire familiarità con alcuni elementi di base della statistica. Questi includono:
- Media aritmetica (media semplice): Si calcola sommando tutti i valori di un insieme di dati e dividendo la somma per il numero totale di valori.
- Ponderazione: Si assegna un peso a ciascun valore in base alla sua importanza relativa nel contesto specifico.
La media ponderata è utilizzata quando si vuole calcolare una media che prende in considerazione l’importanza relativa dei diversi valori. La formula per calcolare la media ponderata è:
![]()
dove:
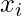 rappresenta i valori nell’insieme di dati,
rappresenta i valori nell’insieme di dati,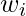 indica i pesi corrispondenti ai valori,
indica i pesi corrispondenti ai valori,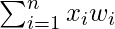 è la somma dei prodotti dei valori per i loro pesi,
è la somma dei prodotti dei valori per i loro pesi,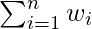 è la somma di tutti i pesi.
è la somma di tutti i pesi.
Varianza e deviazione standard: Questi due concetti misurano quanto i valori di un insieme di dati si discostano dalla media. La deviazione standard è la radice quadrata della varianza e fornisce un’indicazione della dispersione dei dati.
- Varianza: La media dei quadrati delle differenze tra ogni valore e la media aritmetica.
- Deviazione standard: Radice quadrata della varianza.
Per concludere, la comprensione di questi concetti è fondamentale per analizzare e interpretare qualsiasi insieme di dati nel contesto della media ponderata online.
Software educativi per l’insegnamento delle medie ponderate
I software educativi sono strumenti digitali progettati per facilitare l’apprendimento e l’insegnamento di concetti specifici. Nel contesto delle medie ponderate, questi programmi consentono agli studenti di comprendere meglio come calcolare la media di un insieme di numeri che hanno differenti pesi o importanze.
Caratteristiche principali dei software:
- Interfaccia utente intuitiva: garantisce che gli studenti possano navigare facilmente tra le varie funzioni del software.
- Esempi pratici: fornisce casi di studio che dimostrano l’applicazione delle medie ponderate in scenari reali.
- Esercizi interattivi: permette agli studenti di praticare con esercitazioni che ricevono feedback immediati.
Software raccomandati:
- MathPad: un’applicazione per iPad che consente di creare documenti contenenti espressioni matematiche e forme geometriche.
- MathPapa: una calcolatrice online che offre soluzioni passo-passo per problemi di algebra, oltre a lezioni e esercizi per aiutare a padroneggiare l’algebra.
- Mathigon: una piattaforma educativa interattiva che offre strumenti gratuiti, corsi e attività per rendere l’apprendimento della matematica più coinvolgente.
- WeightedAverage ToolKit: Include moduli di apprendimento specifici per campi come statistica ed economia.
- EduWeight: Integra videogiochi educativi per un apprendimento più coinvolgente.
| Software | Caratteristiche | Liv
ello di istruzione |
|---|---|---|
| MathPond | Esercizi personalizzabili, feedback immediato | Tutti i livelli |
| WeightedAverage ToolKit | Moduli statistica, esercizi specifici campo economico | Superiore |
| EduWeight | Videogiochi integrati, interfaccia utente coinvolgente | Medie Superiori |
Gli insegnanti possono sfruttare questi software per creare lezioni più interattive e personalizzate in base alle esigenze degli studenti, mentre gli studenti possono utilizzare gli strumenti per rinforzare la propria comprensione del concetto di media ponderata attraverso la pratica autonoma e la ricezione di feedback istantanei.
Analisi e interpretazione di dati ponderati
L’analisi di dati ponderati avviene quando si attribuisce un peso diverso a ciascuna unità di un insieme di dati in base alla loro rilevanza o importanza. Ciò è spesso necessario in indagini e ricerche statistiche quando alcuni dati sono più influenti o significativi di altri.
Durante l’interpretazione, i pesi influenzano il risultato delle statistiche descrittive, come la media ponderata. La media ponderata si calcola moltiplicando il valore di ciascun dato per il suo peso e sommando i prodotti ottenuti, per poi dividere il totale per la somma dei pesi.
Ecco una tabella che illustra un semplice set di dati ponderati:
| Dato | Peso | Valore Ponderato |
|---|---|---|
| 5 | 2 | 10 |
| 3 | 1 | 3 |
| 8 | 3 | 24 |
In questo caso, la somma dei prodotti dei valori ponderati è 37 e la somma dei pesi è 6. Pertanto, la media ponderata è 37/6, che equivale a circa 6.17.
L’analisi statistica avanzata può includere la regressione lineare ponderata, dove i pesi sono utilizzati per minimizzare l’impatto di outliers o aumentare la rilevanza di alcuni dati nella determinazione della linea di tendenza.
Gli strumenti di analisi dei dati ponderati sono di vitale importanza in campi come l’economia e la sociologia, dove si tengono in considerazione fattori come la stratificazione o il disegno del campione. È cruciale comprendere i metodi di ponderazione e il loro impatto sull’interpretazione dei dati per trarre conclusioni accurate dalla ricerca.
Privacy e Sicurezza dei Dati nella Media Ponderata Online
La media ponderata online fa riferimento all’uso di algoritmi che assegnano pesi diversi a vari elementi per calcolare una media, spesso utilizzata in ambiti come valutazioni o sondaggi. In questo contesto, la privacy si riferisce al diritto degli individui di mantenere le proprie informazioni personali al sicuro e private. La sicurezza dei dati riguarda le misure e i protocolli implementati per proteggere le informazioni digitali dai rischi, come accessi non autorizzati o cyberattacchi.
I dati raccolti per la media ponderata online possono includere:
- Informazioni personali: nome, età, sesso.
- Dati relativi alle valutazioni: risposte a sondaggi o test.
Per proteggere tali dati, le organizzazioni devono attuare strategie di sicurezza quali:
- Crittografia: Rendi i dati illeggibili senza una chiave di decifrazione.
- Autenticazione: Verifica l’identità degli utenti prima di concedere l’accesso.
- Backup: Conserva copie di sicurezza per prevenire perdite di dati.
Le leggi sulla privacy dei dati, come il GDPR nell’Unione Europea, impongono agli operatori online di adottare misure per garantire il trattamento sicuro delle informazioni personali. Questo include la notifica agli utenti su come i loro dati saranno utilizzati e l’ottenimento del consenso per la raccolta e il trattamento delle informazioni.
Tabella riepilogativa delle misure di sicurezza:
| Misura di sicurezza | Descrizione | Obiettivo |
|---|---|---|
| Crittografia | Offuscare i dati | Prevenire la lettura non autorizzata |
| Autenticazione | Verificare identità | Controllare accessi ai dati |
| Backup | Creare copie di sicurezza | Salvaguardare contro perdite |
| Legislazione | Conformità alle normative | Garantire trattamento legittimo |
È fondamentale che le organizzazioni mantengano una costante vigilanza nel monitorare e aggiornare le misure di sicurezza per rispondere alle minacce emergenti del panorama digitale.
Tendenze future della media ponderata online
La media ponderata online è una tecnica statistica utilizzata per calcolare una media che tiene conto dell’importanza relativa di ciascun valore. Nel contesto digitale, questa metodologia viene applicata in vari ambiti, come l’analisi dei dati degli utenti, il rating di prodotti e servizi, e la personalizzazione dei contenuti.
Personalizzazione Avanzata: L’uso di algoritmi predittivi per la personalizzazione dei contenuti è previsto intensificarsi. I sistemi saranno in grado di assegnare pesi dinamicamente ai dati in base al comportamento in tempo reale degli utenti.
Integrazione con l’Intelligenza Artificiale: L’integrazione della media ponderata con modelli di intelligenza artificiale per il trattamento di grandi volumi di dati richiederà algoritmi ancora più sofisticati per affinare l’accuratezza delle previsioni.
| Area Di Impiego | Impatto Previsto |
|---|---|
| Analisi Dati | Maggiore precisione nella segmentazione |
| Marketing | Personalizzazione mirata delle campagne |
| Educazione | Valutazioni più equilibrate e rappresentative |
Trasparenza e Etica: Con l’aumento della complessità degli algoritmi, si prevede una maggiore richiesta di trasparenza e standard etici per prevenire distorsioni e bias dei dati.
Decisioni Basate su Dati: Le aziende continueranno a sfruttare la media ponderata per informare le decisioni strategiche cercando di trarre il massimo vantaggio dall’analisi dei dati.
Sviluppo di Nuovi Strumenti: Emergeranno nuovi strumenti specifici per ottimizzare la media ponderata online, che supportino le organizzazioni nell’esame dei big data.
In definitiva, si assiste a un’evoluzione costante delle applicazioni della media ponderata online, mirate a migliorare l’accuratezza decisionale in diversi campi.