Calcolare la trasformata di Laplace
Written by: H. Candido on 2024-06-11
La trasformata di Laplace è uno strumento matematico utilizzato nell’analisi dei sistemi dinamici. Essa consente di trasformare una funzione definita nel dominio del tempo (spesso indicata come t) in una funzione nel dominio della frequenza o complesso (indicata con s). Questa trasformazione è particolarmente utile per semplificare la risoluzione di equazioni differenziali.
La notazione standard per la trasformata di Laplace di una funzione f(t) è data da:
L{f(t)} = F(s)
Dove:
- L indica l’operatore di Laplace,
- f(t) è la funzione originale nel dominio del tempo,
- F(s) è la funzione trasformata nel dominio di Laplace.
Applicazioni:
- Risoluzione di equazioni differenziali
- Analisi e controllo di sistemi
- Studi di stabilità
La trasformata di Laplace è definita come:
![]()
dove e è la base dei logaritmi naturali. La funzione ![]() è nota come il nucleo della trasformata di Laplace.
è nota come il nucleo della trasformata di Laplace.
Elementi chiave:
- Linearità: Se f(t) e g(t) hanno trasformate di Laplace, allora per qualsiasi coppia di costanti
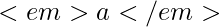 e
e 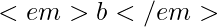 , si ha che
, si ha che 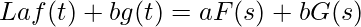 .
. - Trasformazione dell’integrale: La trasformata di Laplace dell’integrale di
- una funzione è uguale al rapporto tra la trasformata della funzione e s.
- Trasformazione della derivata: La trasformata di Laplace della derivata di una funzione è s moltiplicato per la trasformata della funzione, meno il valore iniziale della funzione.
La trasformata è particolarmente efficace per analizzare sistemi lineari e invarianti nel tempo e viene comunemente applicata in ingegneria, fisica e matematica. Online si trovano molteplici risorse che offrono calcolatori per la trasformata di Laplace, facilitando lo studio e l’applicazione di questo metodo analitico.
Calcolatore Trasformata di Laplace
Definizione e Teoria di Base
La trasformata di Laplace è uno strumento matematico che trasforma una funzione di tempo in una funzione di una variabile complessa. Viene comunemente utilizzata per analizzare i sistemi dinamici e risolvere equazioni differenziali.
Integrali e Formula della Trasformata di Laplace
La trasformata di Laplace di una funzione ![]() , definita per
, definita per ![]() , è data dall’integrale:
, è data dall’integrale:
![Rendered by QuickLaTeX.com \[\mathcal{L}{f(t)}(s) = \int_0^\infty e^{-st} f(t) , dt\]](https://calcolo.online/wp-content/ql-cache/quicklatex.com-0b735fb4c8d6d351d718af10d84387be_l3.png)
dove:
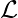 denota la trasformata di Laplace,
denota la trasformata di Laplace,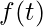 è la funzione di tempo,
è la funzione di tempo,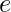 è la base dei logaritmi naturali,
è la base dei logaritmi naturali,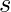 è una variabile complessa,
è una variabile complessa, 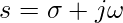 ,
,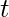 rappresenta il tempo.
rappresenta il tempo.
La condizione di esistenza di questa trasformata richiede che l’integrale converga, ovvero che ( f(t) ) sia integrabile nel range di integrazione.
Proprietà Fondamentali
La trasformata di Laplace possiede diverse proprietà che ne facilitano l’applicazione. Di seguito sono elencate alcune delle proprietà fondamentali:
Linearità:
Se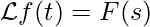 e
e 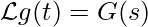 , allora
, allora 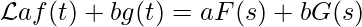 , con
, con 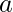 e
e 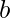 costanti reali.
costanti reali.Trasformata della derivata:
Se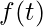 e le sue derivate fino all’ordine
e le sue derivate fino all’ordine 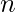 sono trasformabili, allora
sono trasformabili, allora 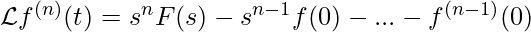 .
.Teorema del valore iniziale:
Se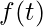 e
e 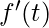 sono trasformabili e
sono trasformabili e 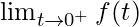 esiste finitamente, allora
esiste finitamente, allora 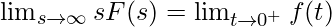 .
.
Queste proprietà sono fondamentali per semplificare il processo di trasformazione e per l’analisi di funzioni complesse nel dominio della frequenza.
Applicazioni Pratiche
La trasformata di Laplace è uno strumento matematico potente utilizzato per semplificare la risoluzione delle equazioni differenziali e l’analisi dei sistemi lineari.
Risolvere equazioni differenziali
Le equazioni differenziali descrivono una vasta gamma di fenomeni fisici, ingegneristici e matematici. La trasformata di Laplace converte equazioni differenziali, che sono funzioni del tempo, in equazioni algebriche più semplici per risolverle nel dominio della frequenza. Questo metodo è particolarmente utile per equazioni differenziali lineari con condizioni iniziali note.
Analisi dei sistemi lineari
I sistemi lineari sono costituiti da componenti che si comportano secondo principi lineari, come circuiti elettrici, sistemi di controllo e strutture meccaniche. La trasformata di Laplace è fondamentale nell’analisi delle funzioni di trasferimento, che descrivono la risposta di un sistema all’ingresso di segnali.
Utilizzare la trasformata di Laplace per l’analisi dei sistemi lineari aiuta a prevedere il comportamento dei sistemi senza richiedere la soluzione temporale diretta delle equazioni differenziali.
Strumenti online per la trasformata di Laplace
La trasformata di Laplace è uno strumento matematico utilizzato per trasformare funzioni del tempo in funzioni della variabile complessa. L’operazione facilita l’analisi dei sistemi dinamici nel dominio della frequenza.
I strumenti online offrono agli utenti la possibilità di calcolare automaticamente la trasformata di Laplace, senza la necessità di complessi calcoli manuali. Questi strumenti sono accessibili da qualsiasi dispositivo con connessione internet e sono particolarmente utili per studenti e ingegneri che cercano soluzioni rapide ed efficienti.
| Strumento | Caratteristiche |
|---|---|
| Mathway | Interfaccia utente intuitiva, fornisce anche passaggi di risoluzione |
| Symbolab | Offre una spiegazione passo-passo dei calcoli, utilizzabile come risorsa didattica |
| Wolfram Alpha | Potente motore di calcolo, fornisce risposte dettagliate e visualizzazioni |
| Integral Calculator | Specializzato in calcoli integrali, inclusa la trasformata di Laplace, con possibilità di visualizzare il grafico |
Gli strumenti sono generalmente gratuiti, ma potrebbero avere funzionalità premium per utenti che desiderano servizi avanzati. Essi supportano una vasta gamma di funzioni e consentono l’analisi di equazioni differenziali, sistemi di controllo e molto altro.
Un esempio di utilizzo è la semplificazione dell’analisi di circuiti elettrici. Invece di risolvere complesse equazioni differenziali, si può utilizzare la trasformata di Laplace per lavorare con funzioni algebriche più maneggevoli.
Gli strumenti offrono una risorsa preziosa per la comprensione e l’applicazione della trasformata di Laplace in vari campi dell’ingegneria e della scienza.
Tutorial e guide interattive
Il processo di apprendimento della trasformata di Laplace può essere notevolmente facilitato dall’uso di tutorial e guide interattive disponibili online. Queste risorse didattiche offrono agli utenti l’opportunità di visualizzare e interagire con il concetto matematico in modo dinamico e coinvolgente.
Le guide interattive offrono solitamente esempi pratici in cui l’utente può inserire una funzione tempo-dipendente e osservare immediatamente la corrispondente trasformata di Laplace. Attraverso esercizi interattivi, la comprensione della mappatura da una funzione del tempo a una funzione della variabile complessa ( s ) diventa più intuitiva.
Siti web utili:
| Sito Web | Caratteristiche |
|---|---|
| LaplaceInteractive | Visualizzazioni, esempi variabili, quiz |
| TransformCalc | Calcolatrice interattiva, passaggi dettagliati |
| MathTutor | Lezioni video, test interattivi |
Alcuni tutorial online includono:
- Video spiegazioni: Spezzano i concetti complessi in segmenti più semplici, rendendo lo studio più gestibile.
- Quiz Formativi: Consentono di mettere alla prova la comprensione dell’argomento e ricevere feedback immediati.
- Diagrammi e Grafici: Aiutano a visualizzare relazioni e teoremi cruciali per la trasformata.
È consigliabile, per chi inizia, di avvalersi di risorse che progressivamente conducano dall’introduzione dei principi base fino alla risoluzione di esercizi più complessi. Inoltre, molte di queste risorse sono personalizzabili, permettendo agli utenti di esplorare vari scenari e strutturare il proprio percorso di apprendimento.
Esercizi risolti e esempi
La trasformata di Laplace è uno strumento matematico che trasforma una funzione del tempo in una funzione della variabile complessa s. Gli esercizi risolti qui sotto mostrano come applicare la trasformata a diverse funzioni.
Esempio 1: Trasformata di una funzione costante
Data la funzione costante f(t) = 3, la sua trasformata di Laplace è:
![Rendered by QuickLaTeX.com \[L{f(t)} = \int_{0}^{+\infty} e^{-st} \cdot 3 dt = \frac{3}{s} \quad \text{per} \quad Re(s) > 0\]](https://calcolo.online/wp-content/ql-cache/quicklatex.com-5a06f66e67a5da5ea1ad2bab712842cc_l3.png)
Esempio 2: Trasformata di una funzione esponenziale
Per la funzione exponenziale f(t) = e^{-2t}, la trasformata di Laplace è calcolata come segue:
![Rendered by QuickLaTeX.com \[L{f(t)} = \int_{0}^{+\infty} e^{-st} \cdot e^{-2t} dt = \frac{1}{s + 2} \quad \text{per} \quad Re(s) > -2\]](https://calcolo.online/wp-content/ql-cache/quicklatex.com-5fed98c2a5cff4aa667d7d1b6ec6e02f_l3.png)
Tabella di alcune trasformate di Laplace comuni:
| Funzione di tempo f(t) | Trasformata di Laplace L{f(t)} |
|---|---|
| 1 | 1/s |
| t^n (n intero positivo) | n!/s^(n+1) |
| e^{at} | 1/(s-a) |
| sin(at) | a/(s^2 + a^2) |
| cos(at) | s/(s^2 + a^2) |
Per approfondire la comprensione del concetto, si consiglia di risolvere esercizi progressivamente più complessi, incrementando gradualmente anche la varietà delle funzioni da trasformare.
Tavole della Trasformata di Laplace
La trasformata di Laplace è uno strumento matematico utilizzato per trasformare una funzione del tempo in una funzione della variabile complessa s. Le tavole della trasformata di Laplace sono raccolte di equazioni che correlano una funzione nel dominio del tempo alla sua corrispettiva nel dominio della frequenza.
Una tavola tipica di trasformate di Laplace presenta una colonna per la funzione nel tempo (f(t)) e una colonna per la rispettiva trasformata di Laplace (F(s)). Ecco un esempio semplificato di come potrebbe essere presentata una tavola:
| f(t) (tempo) | F(s) (Trasformata di Laplace) |
|---|---|
| 1 (costante) | 1/s |
| t (tempo) | 1/s^2 |
| e^(-at) (espon.) | 1/(s+a) |
| cos(ωt) (coseno) | s/(s^2 + ω^2) |
| sin(ωt) (seno) | ω/(s^2 + ω^2) |
Le trasformate sono particolarmente utili nell’analisi dei sistemi lineari e invarianti nel tempo, semplificando lo studio delle equazioni differenziali. Grazie all’utilizzo delle tavole, l’ingegnere o lo scienziato può rapidamente identificare la trasformata di una funzione di interesse senza dover calcolare l’integrale di trasformazione.
È importante notare che le tavole della trasformata di Laplace disponibili in letteratura possono variare per l’insieme di funzioni presentato. Alcune tavole possono estendersi a includere funzioni più complesse e le rispettive trasformate, utili in campi di ingegneria più avanzati come il controllo automatico e l’ingegneria elettrica.
Metodi numerici e approcci computazionali
Nell’ambito della trasformata di Laplace, i metodi numerici e gli approcci computazionali giocano un ruolo cruciale per facilitare l’analisi e la soluzione di equazioni differenziali lineari. Tali metodi permettono di approssimare la trasformata di Laplace e la sua inversa attraverso l’uso di algoritmi.
Algoritmi di Approssimazione: Tra i comuni algoritmi numerici vi sono quelli iterativi come il metodo di Bromwich per la trasformata inversa, che si basa sul calcolo di un’integrale complesso.
Metodi Basati su Serie:
- Metodo di Euler: Utilizza le espansioni in serie di funzioni.
- Metodo dei Momenti: Stima i valori prendendo le somme finite dei momenti.
Strumenti Computazionali:
- Software di Calcolo: MATLAB e Mathematica sono esempi di software che dispongono di funzioni integrate per la trasformata di Laplace.
- Calcolatori Online: Esistono piattaforme web che forniscono strumenti per la calcolo diretto e inverso della trasformata.
Impatto dell’Errore Numerico: In tutti questi metodi, è importante tener conto dell’errore numerico e stabilire criteri di accuratezza.errno_rmse
| Metodo | Descrizione | Utilizzo |
|---|---|---|
| Bromwich | Integrale inverso su contorno complesso | Equazioni differenziali |
| Euler | Serie di potenze | Problemi al valore iniziale |
| Metodo dei Momenti | Somme finite di momenti | Problemi al contorno |
| Calcolatori Online | Piattaforme per trasformata dirette/inverse | Uso didattico e rapido |
I metodi numerici riescono così a fornire soluzioni accurate in contesti in cui la soluzione analitica è complessa o inesistente. L’approccio computazionale, integrando l’uso del calcolo numerico, permette di estendere l’applicabilità della trasformata di Laplace a un’ampia varietà di problemi ingegneristici e fisici.
Software e pacchetti per calcoli scientifici
Nel campo dell’analisi numerica, diversi software sono strumentali per effettuare la trasformata di Laplace. Questi pacchetti comprendono tanto applicazioni desktop quanto risorse online. MATLAB è un ambiente integrato che permette di eseguire calcoli intensivi e viene ampiamente utilizzato in ingegneria e fisica. Offre la funzione laplace per trasformazioni simboliche. Alternativamente, Mathematica dispone di capacità simboliche avanzate e include il comando LaplaceTransform.
Per l’uso nel settore educativo o per chi cerca alternative a costo zero, Octave rappresenta un’ottima scelta come software gratuito che è compatibile con i comandi di MATLAB. Inoltre, SciPy, una libreria di Python per il calcolo scientifico, include il modulo signal che ha funzionalità per la trasformata di Laplace.
Di seguito si trova una tabella riassuntiva dei software:
| Software/Pacchetto | Tipo | Comando/Funzione per Trasformata di Laplace |
|---|---|---|
| MATLAB | A pagamento | laplace |
| Mathematica | A pagamento | LaplaceTransform |
| Octave | Gratuito | Compatibile con i comandi di MATLAB |
| SciPy (Python) | Gratuito | signal (modulo) |
Per calcoli online, ci sono siti web come Wolfram Alpha che permettono di realizzare calcoli simbolici attraverso un’interfaccia utente web. Questi strumenti sono particolarmente utili per studenti e professionisti che necessitano di una verifica rapida dei loro risultati.
Forum di Discussione e Comunità Online
I forum di discussione rappresentano uno spazio virtuale in cui gli individui possono scambiarsi informazioni, porre domande e offrire assistenza riguardo a un argomento specifico, in questo caso, la trasformata di Laplace. Gli utenti possono registrarsi per partecipare attivamente alle conversazioni, condividere le loro conoscenze o semplicemente leggere gli interventi altrui per ampliare la propria comprensione dell’argomento.
Principali piattaforme:
- Math Forum: Questo forum è apprezzato per la sua comunità di esperti in matematica che forniscono risposte approfondite.
- Reddit: Un subreddit dedicato può essere utilizzato per discussioni informali e richieste di aiuto.
Componenti utili dei forum:
- FAQ: Sezioni con risposte alle domande frequenti aiutano gli utenti a trovare rapidamente soluzioni a problemi comuni.
- Thread o Discussioni: Sequenze di messaggi ordinati cronologicamente dove gli utenti discutono una specifica questione.
- Messaggi Pubblici e Privati: Opzioni per discutere pubblicamente o in privatezza.
Le community online includono il vantaggio della partecipazione di persone da tutto il mondo, favoriscono la collaborazione e l’interazione indipendentemente dalla posizione geografica dei partecipanti.
Si avverte l’utente di valutare criticamente le informazioni reperite nei forum, dato che i contributi sono forniti da membri della comunità con diverse competenze e livelli di esperienza.
Tabella di confronto tra forum:
| Forum | Punto di Forza | Modalità di Accesso |
|---|---|---|
| Math Forum | Esperti in matematica | Registrazione |
| Discussione informale | Libero/Registrazione |
Ultime ricerche e sviluppi
Le recenti indagini sulla Trasformata di Laplace si concentrano sull’ottimizzazione degli algoritmi per il calcolo online, consentendo una più rapida risoluzione di problemi ingegneristici e matematici. Gli sviluppi in questo ambito includono l’implementazione di nuovi software, che facilitano l’utilizzo della trasformata da parte di studenti e professionisti.
Un esempio significativo è l’uso dell’intelligenza artificiale (IA) per migliorare la computazione delle trasformate di funzioni complesse. L’IA permette l’analisi di un numero maggiore di punti dati, riducendo gli errori nell’approssimazione e velocizzando il processo di calcolo.
| Innovazione | Descrizione |
|---|---|
| Algoritmi Migliorati | Riduzione della complessità computazionale nei nuovi algoritmi. |
| Software Personalizzabile | Aumento delle opzioni di personalizzazione per l’utente. |
| Interfacce Intuitive | Sviluppo di interfacce più intuitive e accessibili. |
| Integrazione con altre TDC | Implementazione di funzionalità di integrazione con altre trasformate di dominio della frequenza. |
La ricerca si focalizza anche sull’integrazione della Trasformata di Laplace con altri strumenti di calcolo online, come simulazioni al computer e piattaforme di apprendimento automatico, per una modellazione più olistica dei sistemi dinamici.
In sintesi, il progresso tecnologico sta avendo un impatto significativo sull’applicazione della Trasformata di Laplace nel campo dell’ingegneria e oltre, introducendo metodi più efficienti e accessibili per l’analisi dei sistemi e il trattamento dei segnali.
FAQ e Domande Comuni
Cos’è la trasformata di Laplace?
La trasformata di Laplace è una tecnica matematica usata per trasformare una funzione del tempo in una funzione della frequenza. È spesso applicata per risolvere equazioni differenziali.
Come si calcola la trasformata di Laplace online?
Per calcolare la trasformata online, inserire l’equazione nella barra di ricerca di un calcolatore di trasformata online e premere il pulsante di calcolo.
| Passi | Azione |
|---|---|
| Inserimento equazione | Digitare l’equazione differenziale. |
| Selezionare l’operazione | Scegliere ‘Calcola la trasformata di Laplace’. |
| Risultato | Visualizzare la soluzione trasformata. |
Quali sono le applicazioni della trasformata di Laplace?
L’applicazione principale è nella risoluzione di equazioni differenziali lineari. Vengono utilizzate anche in ingegneria del controllo, fisica, matematica e altre discipline scientifiche.
È sicuro usare strumenti online per il calcolo della trasformata di Laplace?
Gli strumenti online sono generalmente sicuri se provengono da fonti affidabili. Bisogna assicurarsi che il sito web offra protezione dei dati e non condivida informazioni senza consenso.
I calcolatori online sono accurati?
I calcolatori online per la trasformata di Laplace sono accurati se programmati correttamente. Verificare la recensioni di altri utenti e testarli con equazioni note per confermarne l’affidabilità.