Definizione di determinante

Il concetto di determinante è fondamentale nell’algebra lineare. Si tratta di un valore scalare che può essere calcolato da una matrice quadrata. Il determinante di una matrice A, indicato con det(A) o |A|, riflette certe proprietà algebriche della matrice. In particolare, il determinante aiuta a determinare se un sistema di equazioni lineari è risolvibile, ed è anche un indicatore per capire se la matrice è invertibile; una matrice è non invertibile se il suo determinante è zero.

Per matrici di piccole dimensioni, il calcolo del determinante è relativamente semplice:

Per una matrice 2×2:
$A = \begin{bmatrix} a & b \\ c & d \end{bmatrix}$
$\text{det}(A) = ad - bc$
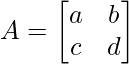
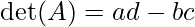
Per una matrice 3×3, usando la Regola di Sarrus o il metodo dei cofattori:
$A = \begin{bmatrix} a & b & c \\ d & e & f \\ g & h & i \end{bmatrix}$
$\text{det}(A) = aei + bfg + cdh - ceg - bdi - afh$

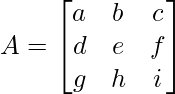
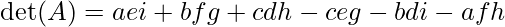
Per matrici di ordine superiore, il calcolo diventa più complesso e solitamente si ricorre a metodi come lo sviluppo di Laplace o l’utilizzo di algoritmi specifici per il calcolo dei determinanti.

Il determinante ha diverse proprietà significative. Ad esempio, il determinante di una matrice è uguale al prodotto dei suoi autovalori, ciascuno moltiplicato per la sua molteplicità algebrica. Inoltre, il determinante del prodotto di due matrici è uguale al prodotto dei determinanti delle due matrici.

Calcolatore Determinante Matrice

Proprietà dei determinanti

Il determinante di una matrice fornisce informazioni significative sul comportamento della matrice stessa, come l’invertibilità o il volume distorto nello spazio da una trasformazione lineare. Le seguenti proprietà sono fondamentali per la comprensione e il calcolo dei determinanti.

Invarianza per trasposizione

Il determinante di una matrice A è uguale al determinante della sua trasposta A^T. Formalmente, se A è una matrice quadrata di ordine n, allora:

$\det(A) = \det(A^T)$

Questa proprietà indica che l’orientamento delle righe e delle colonne non influisce sul valore del determinante.

Multilinearità

Il determinante è una funzione multilineare rispetto alle righe o alle colonne di una matrice. Questo implica due condizioni principali:

Il determinante è proporzionale a ciascuna riga o colonna della matrice. Se una riga o colonna è moltiplicata per uno scalare k, il determinante della nuova matrice risulta moltiplicato per k.
Se a una riga (o colonna) di una matrice si aggiunge un’altra riga (o colonna) moltiplicata per uno scalare, il determinante non cambia.

Comportamento rispetto alle operazioni elementari

Le operazioni elementari di riga modificano il determinante in modi prevedibili:

Scambiare due righe moltiplica il determinante per -1.
Moltiplicare una riga per uno scalare non zero cambia il determinante moltiplicandolo per lo stesso scalare.
Aggiungere a una riga un multiplo scalare di un’altra non altera il valore del determinante.

Queste regole sono utili per semplificare il calcolo dei determinanti.

Determinante di una matrice triangolare

Il determinante di una matrice triangolare è il prodotto degli elementi sulla diagonale principale. Se T è una matrice triangolare, sia superiore sia inferiore, il suo determinante è:

$\det(T) = t_{11} \cdot t_{22} \cdot ... \cdot t_{nn}$

Dove $t_{ii}$ sono gli elementi sulla diagonale principale di T. Questo rende il calcolo dei determinanti particolarmente semplice in tale caso.

Metodi di calcolo

Per il calcolo del determinante di una matrice, sono disponibili vari metodi che si differenziano per complessità e applicabilità in base alle dimensioni della matrice. I seguenti sono tra i più utilizzati in ambito algebrico.

Regola di Sarrus

La Regola di Sarrus è applicabile esclusivamente a matrici 3×3. Il determinante si ottiene sommando i prodotti delle diagonali principali e sottraendo i prodotti delle diagonali che si estendono dal basso verso l’alto. Di seguito è illustrato il procedimento:

Prolungare visivamente le prime due colonne della matrice 3×3 accanto alla matrice stessa.
Moltiplicare gli elementi lungo le tre diagonali da sinistra verso destra e sommare i risultati.
Moltiplicare gli elementi lungo le tre diagonali da destra verso sinistra e sommare i risultati.
Sottrarre il totale del passo 3 dal totale del passo 2 per ottenere il determinante.

Sviluppo di laplace

Lo Sviluppo di Laplace, utilizzabile su matrici di qualsiasi dimensione, si basa sul concetto dei complementi algebrici. Un determinante viene calcolato come la somma dei prodotti degli elementi di una riga o colonna per i rispettivi cofattori. La procedura è la seguente:

Si sceglie una qualsiasi riga o colonna.
Per ogni elemento, si calcola il determinante della matrice che rimane eliminando la riga e la colonna dell’elemento considerato (sottomatrice).
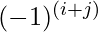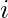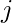Si moltiplica il determinante calcolato per l’elemento originale e per $(-1)^{(i+j)}$ , dove $i$ e $j$ sono rispettivamente l’indice di riga e colonna dell’elemento.
La somma di questi valori fornisce il determinante della matrice originale.

Metodo di riduzione

Il Metodo di Riduzione consiste nel trasformare la matrice in una forma triangolare superiore o inferiore, facilitando così il calcolo del determinante, che sarà pari al prodotto degli elementi della diagonale principale. Il processo include:

Utilizzare operazioni elementari sulle righe come scambio, moltiplicazione di una riga per una costante non zero, e somma tra righe.
Ottenere una matrice triangolare, dove tutti gli elementi al di sotto o al di sopra della diagonale principale sono zeri.
Calcolare il prodotto degli elementi sulla diagonale principale per ottenere il determinante.

Determinante e matrici speciali

Il determinante è una proprietà numerica che può essere associata a matrici quadrate. Si rivela particolarmente interessante nel caso di matrici speciali come quelle diagonali, ortogonali e simmetriche, che presentano caratteristiche uniche in termini di calcolo del determinante.

Determinante di matrici diagonali e scalari

Una matrice diagonale è una matrice quadrata in cui tutti gli elementi al di fuori della diagonale principale sono nulli. Il determinante di una matrice diagonale si ottiene semplicemente moltiplicando gli elementi della diagonale principale.

Esempio di matrice diagonale:

$D = \begin{bmatrix} d_1 & 0 & \cdots & 0 \\ 0 & d_2 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & d_n \end{bmatrix}$

Determinante: $\text{det}(D) = d_1 \cdot d_2 \cdot \ldots \cdot d_n$

Un caso particolare è la matrice scalare, una diagonale in cui tutti gli elementi sulla diagonale principale sono uguali. Il determinante è la potenza dell’elemento diagonale per l’ordine della matrice:

Esempio di matrice scalare: tutti gli 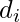$d_i$ sono uguali a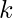 $k$
Determinante: 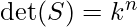$\text{det}(S) = k^n$ , dove 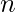$n$ è l’ordine della matrice

Determinante di matrici ortogonali

Una matrice ortogonale è una matrice quadrata la cui trasposta è anche la sua inversa, indicando che le colonne e le righe sono ortogonali (perpendicolari) le une con le altre e hanno lunghezza unitaria.

Condizione: 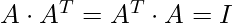$A \cdot A^T = A^T \cdot A = I$ , dove 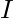$I$ è la matrice identità

Il determinante di una matrice ortogonale può assumere solo due valori: $1$ oppure $-1$ , a prescindere dalle dimensioni della matrice.

Determinante di matrici simmetriche

Una matrice simmetrica è una matrice quadrata che è uguale alla sua trasposta. Ogni elemento $a_{ij}$ è uguale all’elemento $a_{ji}$ .

Proprietà: $A = A^T$

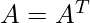
Il calcolo del determinante di una matrice simmetrica segue le regole generali dei determinanti, ma la simmetria può semplificare i passaggi di riduzione nella determinazione del valore.

Determinante e invertibilità

Il determinante di una matrice è un valore chiave nello studio delle proprietà delle matrici e gioca un ruolo cruciale nell’analisi della loro invertibilità.

Teorema di invertibilità delle matrici

Il teorema di invertibilità stabilisce che una matrice quadrata è invertibile se e solo se il suo determinante è diverso da zero. Questa condizione necessaria e sufficiente permette di verificare rapidamente la possibilità di invertire una matrice attraverso il calcolo del determinante. In matematica, si afferma che:

Se det(A) ≠ 0, la matrice A è invertibile.
Se det(A) = 0, la matrice A non è invertibile.

La relazione tra determinante e invertibilità è fondamentale nella risoluzione di sistemi lineari e in altre applicazioni come la decomposizione di matrici.

Calcolo della matrice inversa tramite determinanti

Il calcolo della matrice inversa si basa sul concetto di complementi algebrici e sulla matrice dei cofattori. Per una matrice quadrata A, la matrice inversa A^-1 è data da:

A^-1 = (1/det(A)) * C^T

dove C^T è la trasposta della matrice dei cofattori di A. Gli elementi della matr

Calcolo determinante matrice

Definizione di determinante

Calcolatore Determinante Matrice

Proprietà dei determinanti

Invarianza per trasposizione

Multilinearità

Comportamento rispetto alle operazioni elementari

Determinante di una matrice triangolare

Metodi di calcolo

Regola di Sarrus

Sviluppo di laplace

Metodo di riduzione

Determinante e matrici speciali

Determinante di matrici diagonali e scalari

Determinante di matrici ortogonali

Determinante di matrici simmetriche

Determinante e invertibilità

Teorema di invertibilità delle matrici

Calcolo della matrice inversa tramite determinanti

Calcolatore media ponderata

Calcolatore fattore di scala triangolo

Calcolatore FOIL

Leave a Reply Cancel Reply

Chi siamo

Privacy Policy

Termini di servizio

Cookie policy

Contattaci

CALCOLO.ONLINE