La decomposizione in frazioni parziali è un metodo matematico utilizzato per semplificare l’integrazione di funzioni razionali.
Questa tecnica è particolarmente utile quando si lavora con frazioni il cui numeratore e denominatore sono polinomi.
Il processo di decomposizione consente di esprimere una funzione razionale complessa come la somma di frazioni più semplici, rendendo più agevole l’integrazione o altre operazioni.
Per applicare la decomposizione in frazioni parziali, è necessario che il grado del numeratore sia minore del grado del denominatore.
Se non è così, si svolge una divisione polinomiale per ricondurre la frazione alla forma appropriata.
Una volta ottenuta la forma corretta, si procede identificando i fattori del denominatore.
Questi fattori possono essere polinomi di primo grado, o potenze di polinomi di primo grado, o polinomi irriducibili di grado superiore.
La strategia utilizzata per la decomposizione varia in base alla natura dei fattori nel denominatore:
- Per fattori lineari distinti, ogni frazione avrà un denominatore lineare con un coefficiente da determinare.
- Per fattori lineari ripetuti, ogni frazione conterrà il fattore lineare elevato a un esponente crescente.
- Per fattori quadratici irriducibili, ogni frazione conterrà il fattore quadratico con un numeratore algebrico.
Dopo aver impostato la decomposizione con termini incogniti, si usa l’algebra per determinare i coefficienti delle frazioni.
Questo processo implica solitamente la messa a sistema delle equazioni ottenute eguagliando la funzione decomposta con la funzione originale.
Ecco una rappresentazione generica della decomposizione in frazioni parziali:
( \frac{P(x)}{Q(x)} = \frac{A}{(ax + b)} + \frac{B}{(cx + d)^2} + \frac{Cx + D}{(ex^2 + fx + g)} + … )
Dove:
- ( P(x) ) e ( Q(x) ) sono polinomi.
- ( A, B, C, D, … ) sono coefficienti reali da determinare.
- ( ax + b, cx + d, ex^2 + fx + g, … ) sono i fattori del denominatore.
Condizioni di applicabilità
Per la decomposizione in frazioni parziali di una funzione razionale, è indispensabile che la funzione sia propria, ovvero che il grado del polinomio al numeratore sia inferiore rispetto a quello del denominatore.
Qualora ciò non si verificasse, si procederebbe prima alla divisione polinomiale per ottenere una funzione propria.
Le condizioni specifiche per la decomposizione variano a seconda della natura e della molteplicità delle radici del polinomio al denominatore. Si presenta di seguito una tabella che riepiloga le condizioni principali:
| Tipo di radice | Condizione per la decomposizione |
|---|---|
| Radici semplici | Coefficienti incogniti individuali |
| Radici multiple | Termini frazionari con potenze crescenti del denominatore |
| Radici complesse | Coppie di termini coniugati per ciascuna radice complessa |
Per i polinomi con radici reali semplici, la decomposizione comporta un numero di termini pari al numero di radici, ciascuno con il proprio coefficiente incognito.
Le radici multiple del polinomio denominatore richiedono un termine per ogni molteplicità della radice, ciascuno con la stessa base ma potenze crescenti.
Nel caso di radici complesse non reali, si utilizzano coppie di termini frazionari coniugati.
La decomposizione diviene applicabile solo dopo una dettagliata analisi del polinomio al denominatore.
Sarà quindi necessario fattorizzarlo completamente, individuando la natura delle radici e la loro molteplicità.
Si sottolinea l’importanza di operare in campo complesso per garantire la fattorizzazione completa qualora il polinomio presenti radici immaginarie.
Frazioni parziali e Polinomi
Le frazioni parziali rappresentano una tecnica matematica utilizzata per scomporre funzioni razionali complesse in termini più semplici, facilitandone l’integrazione.
Una funzione razionale si presenta come il rapporto di due polinomi, dove il numeratore e il denominatore sono polinomi in x.
Ad esempio:
[ \frac{N(x)}{D(x)} ]
dove N(x) rappresenta il numeratore e D(x) il denominatore. Si assume che il grado di N(x) sia minore del grado di D(x), altrimenti si procede prima con la divisione polinomiale.
Nella scomposizione, il denominatore D(x) viene fattorizzato in polinomi di grado inferiore.
Le frazioni risultanti, contenenti questi fattori nel denominatore, sono le cosiddette frazioni parziali.
Tipicamente, i tipi di fattori che si considerano sono:
- Polinomi lineari irriducibili (ad esempio, (x – a))
- Potenze di polinomi lineari irriducibili (ad esempio, (x – a)^n)
- Polinomi quadratici irriducibili (ad esempio, ax^2 + bx + c)
- Potenze di polinomi quadratici irriducibili (ad esempio, (ax^2 + bx + c)^n)
Le frazioni ottenute dalla scomposizione possono essere integrate separatamente, spesso risultando in espressioni più gestibili.
La forma generale di una frazione parziale è:
[ \frac{A}{(x – a)^n} \quad o \quad \frac{Bx + C}{(ax^2 + bx + c)^n} ]
dove A, B, e C sono coefficienti da determinare e n è l’ordine del fattore polinomiale nel denominatore.
Tabella dei fattori comuni:
| Fattore nel denominatore | Tipo di frazione parziale corrispondente |
|---|---|
| (x – a) | \frac{A}{(x – a)} |
| (x – a)^n | \frac{A}{(x – a)^n} |
| ax^2 + bx + c | \frac{Bx + C}{ax^2 + bx + c} |
| (ax^2 + bx + c)^n | \frac{Bx + C}{(ax^2 + bx + c)^n} |
Metodo di decomposizione classico
Il metodo di decomposizione classico è una tecnica algebrica utilizzata per spezzare una funzione razionale complessa in componenti più semplici.
Questo processo facilita la risoluzione di integrali indefiniti in particolare nell’analisi matematica.
Per una funzione razionale f(x), il cui numeratore ha grado inferiore rispetto al denominatore, si procede innanzitutto alla sua scomposizione in fratti semplici.
I passaggi seguono un ordine logico:
- Fattorizzare il polinomio denominatore in fattori irriducibili.
- Scrivere una somma di frazioni con numeratore ignoto e denominatore corrispondente a ciascun fattore.
- Determinare i coefficienti dei numeratori risolvendo l’equazione ottenuta dalla somma delle frazioni parziali.
Esempio pratico:
Per una funzione f(x) come segue:
[f(x) = \frac{2x+3}{(x-1)(x+2)}]
La scomposiciòne in frazioni parziali sarebbe:
[f(x) = \frac{A}{x-1} + \frac{B}{x+2}]
Dove A e B sono coefficienti da determinare.
Per determinare i valori di A e B, si moltiplica entrambi i lati dell’equazione per il denominatore comune e si uguaglia il risultato al numeratore della f(x) originale.
Solitamente, si sostituiscono valori di x che annullano i denominatori per trovare più facilmente i coefficienti.
Una volta individuati i valori di A e B, la funzione f(x) originale è espressa come la somma delle sue frazioni parziali, rendendo più agevole l’integrazione termine per termine.
Decomposizione con radici reali semplici
La decomposizione in frazioni parziali con radici reali semplici è applicata quando un polinomio al denominatore si scompone in fattori lineari distinti.
In questo contesto, la funzione razionale viene espressa come somma di frazioni con denominatori corrispondenti ai fattori lineari e numeratori costituiti da costanti da determinare.
Caso radici distinte
Quando un denominatore si scompone in fattori lineari distinti, la decomposizione si esprime nella forma:
A / ( x – r1 ) + B / ( x – r2 ) + … + N / ( x – rn )
dove:
- x rappresenta la variabile della funzione razionale.
- r1, r2, …, rn sono le radici distinte del polinomio al denominatore.
- A, B, …, N sono le costanti numeriche da determinare.
Per trovare i valori delle costanti (A, B, …, N), si può impostare un’equazione dove a sinistra si trova la funzione razionale originale e a destra la somma delle frazioni parziali:
Frazione originale = Decomposizione in frazioni parziali
Moltiplicando entrambi i membri dell’equazione per il denominatore comune, si elimina il denominatore ottenendo un’identità polinomiale. Da questa identità polinomiale si possono ricavare le costanti tramite confronto dei coefficienti o sostituendo valori opportuni di x che annullano i denominatori delle frazioni parziali.
Decomposizione con radici reali multiple
La decomposizione in frazioni parziali con radici reali multiple coinvolge la suddivisione di una funzione razionale in un insieme di frazioni più semplici, che possono essere integrate facilmente.
Caso radici multiple
Quando si ha una funzione razionale in cui il denominatore possiede radici multiple, è necessario adottare un approccio specifico per la decomposizione. Queste radici sono valori per cui il polinomio denominatore diventa zero e si ripetono più di una volta. Per ciascuna radice reale multipla, si assegna una frazione parziale per ogni potenza della radice fino al suo ordine di molteplicità.
Supponiamo di avere una funzione razionale ( R(x) = \frac{P(x)}{Q(x)} ), dove ( P(x) ) e ( Q(x) ) sono polinomi e ( Q(x) ) ha radici reali multiple. Indichiamo con ( r ) una radice del denominatore di molteplicità ( m ). La decomposizione comprende termini della forma ( \frac{A}{(x-r)^k} ), per ogni ( k = 1, 2, …, m ), dove ( A ) è un coefficiente da determinare.
Per esemplificare, se ( Q(x) ) ha una radice ( r ) di molteplicità 3, la decomposizione includerà i termini: ( \frac{A}{(x-r)} ), ( \frac{B}{(x-r)^2} ) e ( \frac{C}{(x-r)^3} ).
Determinare i coefficienti ( A, B, C, \ldots ) può essere realizzato mediante un confronto dei coefficienti dopo aver moltiplicato entrambi i membri dell’equazione per il denominatore comune ( Q(x) ), oppure utilizzando altri metodi come l’integrazione per parti o la sostituzione di valori specifici per ( x ) per semplificare l’espressione.
Decomposizione con radici complesse coniugate
In matematica, la decomposizione in frazioni parziali con radici complesse coniugate si verifica quando si ha una funzione razionale il cui denominatore ha radici non reali che sono coniugate tra loro. Ciò è comune nell’analisi dei sistemi dinamici, nella trasformazione di Laplace e in altre aree dell’ingegneria e della fisica.
Esempio di denominatore con radici complesse coniugate: [ ax^2 + bx + c ]
Le due radici complesse coniugate, indicate con ( \alpha \pm \beta i ), sono il risultato dell’applicazione della formula per risolvere le discriminante negativo delle equazioni quadratiche.
La formula di decomposizione in questo caso prevede l’espressione del numeratore come la somma di due termini. Ognuno di questi termini ha un numeratore formato da due parti: una lineare nella variabile reale e l’altra costante.
Struttura della decomposizione con radici coniugate: [ \frac{Ax + B}{x^2 + px + q} + \frac{Cx + D}{x^2 + px + q} ]
Dove ( A ), ( B ), ( C ), e ( D ) sono costanti reali da determinare.
Il processo per identificare queste costanti richiede di equilibrare i termini sia per la parte reale sia per quella immaginaria, conducente a un sistema di equazioni di cui si dovrà trovare la soluzione.
I valori di ( (A, B, C, D) ) sono spesso calcolati attraverso il metodo di confronto dei coefficienti o, in casi più complessi, sfruttando l’integrazione su un cammino chiuso nel piano complesso.
Tabella dei passaggi chiave per la decomposizione:
| Step | Descrizione |
|---|---|
| 1 | Determinare le radici complesse coniugate del denominatore |
| 2 | Esprimere la funzione razionale come la somma di frazioni con nuovi numeratori |
| 3 | Impostare e risolvere il sistema per trovare le costanti reali del numeratore |
Applicando attentamente questo metodo, si può semplificare l’analisi di funzioni complesse per studi di stabilità e controllo, tra gli altri.
Integrazione di frazioni parziali
L’integrazione di frazioni parziali è un metodo utilizzato per calcolare l’integrale di una funzione razionale, tramite la sua scomposizione in componenti più semplici. Una funzione razionale si definisce come il rapporto di due polinomi. Il processo prevede vari passaggi che dipendono dalla complessità dei polinomi coinvolti.
Scomposizione: La prima fase dell’integrazione di frazioni parziali consiste nello scomporre la funzione razionale in un insieme di frazioni più semplici. Ciò si ottiene individuando i fattori del denominatore e assegnando costanti arbitrarie ai numeratori delle frazioni risultanti.
Ad esempio, considerando una funzione razionale: [ \frac{P(x)}{Q(x)} ]
dove ( P(x) ) e ( Q(x) ) sono polinomi con gradi rispettivamente ( n ) e ( m ), e ( m > n ).
Integrazione: Successivamente, si integrano le frazioni ottenute.
Nel caso in cui il denominatore possieda radici semplici, si ha la seguente forma generale: [ \int \frac{dx}{(ax + b)} = \frac{1}{a} \ln{|ax + b|} + C ]
dove ( a ) e ( b ) non sono zero e ( C ) è la costante di integrazione.
Nel caso in cui vi siano radici multiple, si utilizza la forma: [ \int \frac{dx}{(ax + b)^n} = -\frac{1}{a(n-1)(ax + b)^{n-1}} + C ]
Risultato: Sommando i risultati delle singole integrazioni otteniamo l’integrale della funzione razionale originale.
Utilizzando tali tecniche, una funzione complessa viene ridotta a termini più semplici, rendendo possibile il calcolo dell’area sottesa dalla curva corrispondente. Questo processo è fondamentale in vari campi quali l’ingegneria, la fisica e le scienze applicate.
Esempi di decomposizione
La decomposizione in frazioni parziali permette di scomporre una funzione razionale fratta in somma di frazioni più semplici. Questo metodo è particolarmente utile per l’integrazione di funzioni complesse.
Esempio con radici semplici
Si consideri la funzione razionale fratta: ![]() . La scomposizione in frazioni parziali di questa funzione è la seguente:
. La scomposizione in frazioni parziali di questa funzione è la seguente:
- Determinazione dei coefficienti:
| Denominatore | Frazione Parziale |
|---|---|
| (x+1) | |
| (x-2) |
Dove A e B sono costanti che vanno determinate.
- Soluzione:
Si impone l’uguaglianza: ![]() .
.
Per ![]() , si ha
, si ha ![]() .
.
Per ![]() , si ha
, si ha ![]() .
.
- Risultato: La funzione originale può essere scritta come:
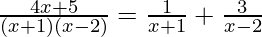 .
.
Esempio con radici multiple
Si prenda in esame la funzione: ![]() . La scomposizione in frazioni parziali verrà eseguita considerando le radici multiple.
. La scomposizione in frazioni parziali verrà eseguita considerando le radici multiple.
- Determinazione dei coefficienti:
| Denominatore | Frazione Parziale |
|---|---|
A, B, e C sono costanti.
- Soluzione:
Si stabilisce l’equazione: ![]() .
.
Si procede alla determinazione dei valori di A, B e C.
Questo può essere fatto confrontando i coefficienti o sostituendo valori particolari di x e risolvendo il sistema di equazioni risultante.
- Risultato:
Dopo aver trovato i valori dei coefficienti, la funzione diventa: ![]() , con A, B, C sostituiti dai rispettivi valori numerici.
, con A, B, C sostituiti dai rispettivi valori numerici.
Esempio con radici complesse
Per la funzione ![]() , ci troviamo di fronte a radici complesse.
, ci troviamo di fronte a radici complesse.
- Determinazione dei coefficienti:
| Denominatore | Frazione Parziale |
|---|---|
A, B, e C sono costanti.
- Soluzione:
La decomposizione coinvolge la ricerca di un polinomio di grado inferiore al denominator nell’espressione di ![]() .
.
Moltiplicando entrambi i membri per il denominatore della funzione originale, si ottiene un’equazione polinomiale che permette di calcolare i valori di A, B, e C.
- Risultato:
Una volta trovati i valore necessari, si ha la scomposizione: ![]() , con valori specifici per A, B e C.
, con valori specifici per A, B e C.
Applicazioni nel Calcolo Integrale
La decomposizione in frazioni parziali è uno strumento potente nel campo del calcolo integrale. Riveste una particolare importanza nella risoluzione di integrali indefiniti di funzioni razionali. La decomposizione consente di trasformare un’integrale complesso in una somma di integrali più semplici.
Si consideri una funzione razionale del tipo:
[ f(x) = \frac{P(x)}{Q(x)} ]
dove ( P(x) ) e ( Q(x) ) sono polinomi e il grado di ( P(x) ) è inferiore a quello di ( Q(x) ).
La prima fase consiste nel dividere la funzione razionale in un insieme di frazioni più semplici. Questa operazione si basa sulla fattorizzazione del denominatore ( Q(x) ).
Esempio di fattorizzazione:
- ( Q(x) = (x-a)^m(x-b)^n )
Dove ( a ) e ( b ) sono radici del polinomio e ( m ), ( n ) sono la loro molteplicità.
In seguito all’applicazione della decomposizione, si può procedere con il calcolo degli integrali dei singoli termini. Le tecniche d’integrazione variano a seconda della natura delle frazioni ottenute.
Lista delle tecniche comuni di integrazione:
- Integrazione diretta
- Sostituzione
- Integrazione per parti
La decomposizione in frazioni parziali semplifica le equazioni e facilita il processo di integrazione.
Uso nel calcolo delle trasformate di Laplace
Le trasformate di Laplace sono uno strumento matematico fondamentale nell’analisi dei sistemi lineari e nel controllo delle loro dinamiche. La decomposizione in frazioni parziali è spesso impiegata per semplificare il calcolo delle trasformate di Laplace inverse, enunciando una funzione complessa come la somma di termini più semplici.
Il processo inizia con una funzione razionale che è il risultato di una trasformata di Laplace, espressa come:
F(s) = N(s) / D(s)
Dove N(s) è il numeratore e D(s) è il denominatore polinomiale. Si assicura che il grado di N(s) sia minore del grado di D(s); altrimenti, si effettua una divisione polinomiale.
L’obiettivo è riscrivere F(s) come una somma di frazioni, ciascuna con un denominatore a primo grado o a secondo grado non fattorizzabile. Per ogni polo di multiplicità m in s = p, si avrà un termine della forma:
A/(s-p) + B/(s-p)² + … + M/(s-p)^m
Per poli complessi coniugati s = a ± jb, i termini vengono espressi in coppia:
(C(s-a) + D)/[(s-a)² + b²]
Una volta completata la decomposizione, si procede al calcolo dell’inversa di ciascun termine separato, impiegando le rispettive trasformate di Laplace inverse note. La funzione del tempo f(t) è poi ottenuta sommando i risultati parziali.
| Polo singolo | Polo multiplo | Poli complessi coniugati |
|---|---|---|
| A/(s-p) | A/(s-p)² | (C(s-a) + D)/[(s-a)² + b²] |
L’utilizzo della decomposizione in frazioni parziali consente di trattare funzioni complesse in maniera più agevole, rendendo più accessibile la risoluzione di equazioni differenziali mediante trasformate di Laplace.
Risorse Addizionali per l’Apprendimento
Le risorse online sono ampiamente disponibili per chi vuole approfondire la decomposizione in frazioni parziali.
I corsi online Coursera e Khan Academy offrono lezioni e esercitazioni che coprono questo argomento nel dettaglio. I libri di testo come Calculus di James Stewart e Advanced Engineering Mathematics di Erwin Kreyszig contengono capitoli dedicati a questi metodi matematici.
Molti forum matematici come Math Stack Exchange e Art of Problem Solving forniscono una piattaforma per la discussione e l’aiuto reciproco su questioni specifiche, incluso questo metodo di integrali.
In aggiunta, accademici e istituti di istruzione offrono documenti e PDF che possono essere scaricati gratuitamente. Questi includono esempi dettagliati e spiegazioni per una migliore comprensione.
| Risorsa | Tipo di Contenuto | Benefici |
|---|---|---|
| Coursera | Video, esercizi | Ampia copertura di argomenti |
| Khan Academy | Video, quiz | Spiegazioni passo-passo |
| Math Stack Exchange | Forum di discussione | Supporto della comunità |
| Art of Problem Solving | Forum, risorse | Focus su matematica avanzata |
| Libri di Testo | Capitoli specifici | Approfondimenti teorici |
Per gli studenti e i professionisti del settore è utile anche utilizzare software matematici come Matlab e Mathematica che possono eseguire la decomposizione in frazioni parziali passo dopo passo.
Questi strumenti possono aiutare a visualizzare e comprendere meglio i processi matematici coinvolti.
Infine, le università spesso mettono a disposizione lezioni registrate e materiale didattico complementare attraverso i loro siti web o piattaforme come edX, dove i corsi possono talvolta essere seguiti gratuitamente.