Convergenza serie online: criteri e strumenti per l'analisi

Definizione di convergenza serie

Una serie è l’espressione della somma infinita dei termini di una sequenza numerica. La convergenza di una serie si verifica quando la somma dei suoi termini tende verso un limite finito, noto come somma della serie. Per determinare se una serie converge, è necessario analizzare il comportamento della successione delle somme parziali $S_n$ , ove $S_n$ rappresenta la somma dei primi n termini di una serie.

Serie Convergente: Una serie ∑ 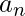$a_n$ si dice convergente se la successione 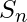$S_n$ ha un limite finito per 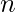$n$ che tende all’infinito, e si scrive: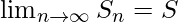
$\lim_{n \to \infty} S_n = S$
Serie Divergente: Una serie ∑ 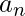$a_n$ è divergente se la successione 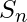$S_n$ non converge verso un limite finito.

Esistono vari criteri per stabilire la convergenza di una serie, tra cui il criterio del confronto, il criterio della radice e il criterio del rapporto. Questi criteri utilizzano confronti con serie di cui si conosce la convergenza o la divergenza per dedurre il comportamento della serie in esame.

Per esempio:

Criterio	Descrizione	Condizione di Convergenza
Criterio del confronto	Confronta la serie con un’altra nota	se ∑ $b_n$ converge e $a_n \leq b_n$
Criterio della radice	Applica la radice n-esima ai termini della serie	se $\lim_{n \to \infty} \sqrt[n]{a_n} < 1$
Criterio del rapporto	Considera il limite del rapporto tra termini consecutivi	se $\lim_{n \to \infty} \frac{a_{n+1}}{a_n} < 1$

La convergenza assoluta si manifesta quando la serie dei valori assoluti dei termini è convergente, condizione più forte che garantisce anche la convergenza della serie originale. In contrasto, una serie può essere condizionatamente convergente se è convergente ma non assolutamente convergente.

Calcolatore convergenza serie

Criteri di convergenza

I criteri di convergenza sono strumenti matematici utilizzati per determinare se una serie infinita converge verso un numero finito. Questi criteri forniscono metodi sistematici per valutare la convergenza di serie complesse.

Criterio del rapporto

Il Criterio del Rapporto stabilisce che per una serie data con termini generali $a_n$ , se esiste un numero $L$ tale che:

$\lim_{{n \to \infty}} \left| \frac{a_{n+1}}{a_n} \right| = L$

e se $L < 1$ , allora la serie converge. Se $L > 1$ o il limite non esiste, la serie diverge.

Criterio della radice

Il Criterio della Radice dice che per una serie con termini generali $a_n$ , se esiste un numero $L$ tale che:

$\lim_{{n \to \infty}} \sqrt[n]{\left| a_n \right|} = L$

e se $L < 1$ , la serie converge. Analogamente al Criterio del Rapporto, se $L > 1$ o il limite non esiste, la serie diverge.

Criterio di Leibniz per serie alternanti

Il Criterio di Leibniz per Serie Alternanti si applica a serie della forma $\sum (-1)^n a_n$ dove ogni termine $a_n$ è non negativo. La serie converge se:

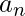$a_n$ è decrescente,
$\lim_{{n \to \infty}} a_n = 0$ .

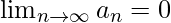Criterio della convergenza assoluta

Infine, il Criterio della Convergenza Assoluta afferma che se la serie dei valori assoluti, $\sum \left| a_n \right|$ , converge, allora anche la serie originale $\sum a_n$ converge. Questo criterio è particolarmente utile perché semplifica la verifica di convergenza per serie con termini sia positivi che negativi.

Convergenza condizionata e assoluta

Una serie è un’espressione matematica composta dalla somma infinita dei termini di una successione. In matematica, per determinare se la somma infinita approda a un valore finito, si studiano i concetti di convergenza condizionata e convergenza assoluta.

Convergenza assoluta significa che la somma dei valori assoluti di tutti i termini della serie è finita. In altri termini, una serie ∑ $a_n$ converge assolutamente se la serie ∑ $|a_n|$ converge. Se una serie converge assolutamente, allora converge anche nel senso usuale (condizionatamente).

Tipologia di serie	Condizione di convergenza
Assoluta	∑ $\|a_n\|$
Condizionata	∑ $a_n$ converge, ma ∑ $\|a_n\|$ non converge

Una convergenza condizionata si verifica quando una serie converge, ma la serie dei valori assoluti dei suoi termini non converge. Per esempio, la serie alternata ∑ $(-1)^n/n$ converge condizionatamente, in quanto la serie dei valori assoluti ∑ $1/n$ diverge.

È importante notare che se una serie converge assolutamente, allora qualsiasi riarrangiamento dei suoi termini preserverà la convergenza al medesimo limite. Invece, la convergenza condizionata non assicura questa proprietà. Un riarrangiamento dei termini di una serie che converge condizionatamente può portare a limiti differenti o persino alla divergenza.

Serie di potenze

Le serie di potenze sono strumenti matematici fondamentali che rappresentano funzioni attraverso somme infinite di termini in potenze di una variabile. Il loro comportamento e le zone di convergenza sono essenziali per diversi campi, tra cui l’analisi complessa e le equazioni differenziali.

Raggio di convergenza

Il raggio di convergenza è un valore che determina l’intervallo in cui una serie di potenze converge verso una funzione. Viene calcolato tramite il criterio di Cauchy-Hadamard, che afferma che il raggio di convergenza $R$ è l’inverso del limite superiore della successione delle radici n-esime dei coefficienti assoluti, vale a dire:

$R = \frac{1}{\lim\sup_{n \to \infty} \sqrt[n]{|a_n|}}$

dove $a_n$ sono i coefficienti della serie. Se il limite non esiste o è infinito, si considera la serie convergente su tutto il campo complesso, con $R = \infty$ .

Convergenza su intervallo di convergenza

La convergenza su intervallo di convergenza si riferisce al comportamento della serie di potenze nell’intervallo definito dal raggio di convergenza. Entro questo intervallo, la serie converge uniformemente e rappresenta una funzione analitica. Fuori dall’intervallo, la serie può divergere o avere punti singolari. L’intervallo di convergenza $I$ è generalmente espresso come:

$I = (x_0 - R, x_0 + R)$

dove $x_0$ è il centro della serie di potenze e $R$ è il raggio di convergenza. La serie può anche essere soggetta a verifica di convergenza nei punti estremali $x_0 - R$ e $x_0 + R$ , poiché il comportamento su tali punti non è assicurato dalla determinazione del raggio.

Teorema del confronto per serie

Il teorema del confronto è uno strumento fondamentale nell’analisi delle serie numeriche. Esso stabilisce una relazione tra due serie in termini di convergenza o divergenza. Quando affrontiamo lo studio della convergenza di una serie, spesso confrontiamo la serie data con una serie nota, utilizzando una delle due principali versioni del teorema:

Teorema del Confronto diretto: Siano ( $a_n$ ) e ( $b_n$ ) due successioni di numeri reali non negativi tali che $a_n \leq b_n$ per ogni $n$ maggiore di un certo $N$ intero positivo.

Se la serie ( 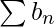$\sum b_n$ ) converge, allora anche la serie ( 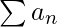$\sum a_n$ ) converge.
Se la serie ( 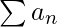$\sum a_n$ ) diverge, allora anche la serie ( 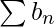$\sum b_n$ ) diverge.

Teorema del Confronto limite: Se $a_n$ e $b_n$ sono successioni di numeri reali positivi e $\lim_{n \to \infty}\frac{a_n}{b_n}$ esiste ed è finito, allora le due serie ( $\sum a_n$ ) e ( $\sum b_n$ ) hanno lo stesso comportamento di convergenza o divergenza.

L’applicazione di questi teoremi richiede la conoscenza di serie di riferimento, come la serie geometrica o la serie armonica, le quali hanno comportamenti di convergenza ben definiti. Il teorema del confronto fornisce una metodologia chiara per determinare la convergenza di serie più complesse, paragonandole con serie più semplici comprendenti termini che fungono da limiti superiori o inferiori.

Convergenza uniforme e puntuale

La convergenza uniforme si verifica quando una serie di funzioni converge verso una funzione limite in modo uniforme per ogni punto nel suo dominio. Formalmente, una successione di funzioni $f_n(x)$ converge uniformemente verso una funzione $f(x)$ su un insieme $D$ se per ogni $\varepsilon > 0$ esiste un numero naturale $N$ tale che per tutti gli $n \geq N$ e per ogni $x \in D$ , si ha che $|f_n(x) - f(x)| < \varepsilon$ .

La convergenza puntuale, invece, richiede che la successione di funzioni $f_n(x)$ converga verso $f(x)$ per ogni punto $x$ del dominio indipendentemente da altri punti. In termini matematici, $f_n(x)$ converge puntualmente verso $f(x)$ se per ogni $\varepsilon > 0$ e per ogni $x \in D$ , esiste un numero naturale $N$ tale che per tutti gli $n \geq N$ , $|f_n(x) - f(x)| < \varepsilon$ .

Ecco una tabella riepilogativa che confronta le due tipologie di convergenza:

Caratteristica	Convergenza uniforme	Convergenza puntuale
Dipendenza da $x$	Indipendente	Dipendente
Validità $\varepsilon - N$	Per tutti $x$ simultaneamente	Per ogni $x$ individualmente
Applicazioni	Continuità, integrazione	Esempi didattici

La distinzione tra convergenza uniforme e puntuale è fondamentale in varie branche dell’analisi, come quella reale e complessa, perché ha implicazioni dirette sulla continuità delle funzioni limite e sulla possibilità di scambiare limiti con integrali o derivate.

Serie di Fourier

Le serie di Fourier rappresentano uno strumento matematico che permette di esprimere una funzione periodica come la somma di funzioni sinusoidali semplici. Queste funzioni sinusoidali, cioè seni e coseni, hanno frequenze che sono multipli interi di una frequenza di base.

Base della Serie di Fourier:

Funzione Periodica: Una funzione f(x) è periodica se esiste un numero P tale che f(x + P) = f(x) per ogni valore di x.
Costruzione della Serie: La serie di Fourier di una funzione periodica f(x) con periodo 2L è definita come:

$f(x) = a_0 + \sum_{n=1}^{\infty} [a_n \cdot \cos(\frac{n\pi x}{L}) + b_n \cdot \sin(\frac{n\pi x}{L})]$

Dove a_0, a_n, e b_n sono coefficienti della serie di Fourier calcolati tramite integrazione della funzione f(x).

Calcolo dei Coefficienti:

Coefficienti a_n: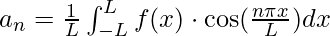
$a_n = \frac{1}{L}\int_{-L}^{L} f(x) \cdot \cos(\frac{n\pi x}{L})dx$
Coefficienti b_n: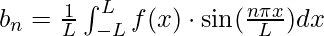
$b_n = \frac{1}{L}\int_{-L}^{L} f(x) \cdot \sin(\frac{n\pi x}{L})dx$

L’importanza delle serie di Fourier risiede nella loro applicabilità in vari campi come l’ingegneria, la fisica e il trattamento dei segnali. Consentono di analizzare le funzioni periodiche nei loro componenti fondamentali, facilitando lo studio dei fenomeni oscillatori. Ad esempio, in elettrotecnica, le serie di Fourier si rivelano essenziali nell’analizzare le correnti alternate e nello sviluppo di circuiti elettrici.

Serie Numeriche

Le serie numeriche sono successioni di numeri che, sommati sequenzialmente, si avvicinano a un valore specifico, noto come limite della serie, se esiste. Queste serie possono essere utilizzate per rappresentare funzioni o risolvere problemi in diversi ambiti della matematica e dell’analisi.

Serie Geometrica

Una serie geometrica è una sequenza di termini in cui ciascun termine successivo si ottiene moltiplicando il precedente per una costante r, chiamata ragione. La serie geometrica converge se il valore assoluto di r è minore di uno e può essere espressa dalla formula:

S = a / (1 – r)

dove S è la somma della serie, e a è il primo termine.

Serie Armonica

La serie armonica è una serie infinita in cui ogni termine è il reciproco di un numero intero positivo. Matematicamente viene rappresentata come:

S = 1 + 1/2 + 1/3 + 1/4 + … + 1/n

Questa serie è nota per la sua divergenza, ovvero non si avvicina a un limite finito all’aumentare di n.

Serie a Termini Positivi

Le serie a termini positivi sono serie numeriche in cui tutti i termini sono maggiori di zero. Un importante criterio utilizzato per determinarne la convergenza è il criterio della radice o di Cauchy, che stabilisce:

Se $\lim_{n \to \infty} (a_n)^{1/n} < 1$ , allora la serie converge.

Dove $a_n$ rappresenta l’n-esimo termine della serie.

Strumenti online per la convergenza serie

I strumenti online per la convergenza serie facilitano l’analisi delle serie matematiche, determinando se sono convergenti o divergenti. Gli utenti possono inserire le serie matematiche e ricevere velocemente una valutazione della loro convergenza. Questi strumenti sono pubblicamente accessibili e spesso gratuiti.

Gli strumenti più noti includono:

Wolfram Alpha: Dotato di un potente motore di calcolo, questo strumento fornisce dettagli sulla convergenza serie e sulla natura delle serie esaminate.
Symbolab: Offre la possibilità di analizzare passaggi individuali del processo di verifica della convergenza, offrendo così un approccio didattico.
Mathway: Concentrato sulla semplicità di utilizzo, permette di determinare rapidamente la convergenza di serie infinite.

L’uso di questi strumenti si articola in diversi passaggi:

Inserire l’equazione della serie.
Selezionare il metodo di verifica della convergenza (ad esempio, il criterio del rapporto, il criterio della radice, il criterio dell’integrale).
Avviare l’analisi.

Essi implementano criteri di convergenza quali:

Criterio del confronto
Criterio del confronto al limite
Criterio della radice
Criterio del rapporto
Criterio dell’integrale
Criterio di Leibniz (per serie alternate)

La tabella seguente mostra alcune differenze chiave tra gli strumenti:

Strumento	Approccio didattico	Semplicità di utilizzo	Dettaglio del risultato
Wolfram Alpha	Medio	Media	Alto
Symbolab	Alto	Media	Medio-Alto
Mathway	Basso	Alta	Medio

Questi servizi sono utili per studenti, insegnanti e professionisti che richiedono una verifica rapida e precisa della convergenza di serie matematiche senza dedicare il tempo necessario per i calcoli manuali.

Applicazioni della convergenza serie in fisica e ingegneria

Le serie sono sequenze di termini matematici che, se sommati, si avvicinano a un valore limite. In fisica e ingegneria, la convergenza di queste serie è fondamentale per diversi motivi:

Analisi di Fourier: Essenziale in fisica, permette di scomporre segnali periodici in componenti sinusoidali. La rappresentazione del segnale come serie di Fourier consente una descrizione accurata delle proprietà del segnale.
Meccanica Quantistica: Le funzioni d’onda sono rappresentate tramite serie. Queste descrivono lo stato di un sistema fisico permettendo di calcolare probabilità di trovarlo in determinate condizioni.

Nella disciplina dell’ingegneria elettrica:

Utilizzo	Descrizione
Circuiti elettrici	Analisi di componenti reattivi (induttori e condensatori) spesso usa serie per la soluzione.
Sistemi di controllo	Progettazione e analisi si basano su serie per descrivere la risposta dei sistemi.

In ingegneria strutturale, le serie possono prevedere il comportamento dinamico delle strutture come ponti e grattacieli, influenzando la progettazione anti-sismica.

Le equazioni differenziali, fondamentali in molte applicazioni di ingegneria, possono essere risolte attraverso lo sviluppo in serie di potenze o altre serie funzionali, permettendo di predire l’evoluzione dei sistemi in studio.

La convergenza delle serie è pertanto un pilastro dell’analisi in fisica e ingegneria, con implicazioni che spaziano dal calcolo delle probabilità al design di sistemi complessi.

Metodi numerici per valutare la convergenza

I metodi numerici forniscono strumenti per stabilire se una serie è convergente o meno. Uno dei metodi più utilizzati è il Test del rapporto: si considera il limite del rapporto tra termini successivi della serie. Se il valore limite è minore di uno, la serie converge.

Un altro strumento è il Test della radice, dove si calcola il limite della radice n-esima del valore assoluto del termine generale. Se il valore limite è minore di uno, allora la serie è convergente.

Tabella dei Metodi comuni:

\lim_{n \to \infty} \left| \frac{a_{n+1}}{a_n} \right| < 1

Metodo	Criterio di Convergenza
Test del rapporto	$\lim_{n \to \infty} \left\| \frac{a_{n+1}}{a_n} \right\| < 1$
Test della radice	$\lim_{n \to \infty} \sqrt[n]{\|a_n\|} < 1$

Occorre precisare che questi test forniscono condizioni sufficienti ma non necessarie: una serie potrebbe essere convergente anche se questi metodi non lo confermano.

È anche importante il Test dell’integrale, che confronta la serie con un integrale definito e determina la convergenza attraverso il comportamento dell’integrale stesso.

Infine, c’è l’Analisi dell’errore. Quando si approssima il valore di una serie convergente tramite somme parziali, l’analisi dell’errore aiuta a stimare la differenza tra la somma parziale calcolata e il valore esatto della serie.

Problemi comuni e errori nella convergenza serie

Nel campo dell’analisi matematica, la convergenza di una serie è la proprietà che permette una somma infinita di termini successivi di approssimare un valore definito. Molti utenti incontrano difficoltà nell’analizzare la convergenza delle serie online a causa di errori comuni.

Prima di esaminare la serie, è essenziale capire la successione dei suoi termini. Se la successione non converge a zero, allora la serie associata non può convergere.

Un errore frequente è l’applicazione scorretta dei criteri di convergenza. Per esempio, il criterio del confronto richiede che i termini della serie siano confrontabili con quelli di una serie nota. Ecco alcuni errori:

Criterio	Errore Comune
Confronto	Omettere la verifica di dominazione di un termine rispetto all’altro.
Rapporto	Ignorare il limite assoluto maggiore di uno.
Radice	Non considerare tutti i limiti superiori del termine sotto radice.

Inoltre, gli utenti spesso dimenticano che una serie a termini positivi che non converge è definita come divergente, mentre per serie che includono anche termini negativi è necessaria un’ulteriore indagine come la convergenza assoluta o la convergenza condizionale.

Un’ulteriore problematica sorge nell’interpretazione dei risultati forniti dagli strumenti online. Occorre accertarsi che l’output sia relativo alla serie analizzata e non a calcoli intermedi o ad altre serie.

Infine, bisogna essere consci che alcuni strumenti online potrebbero non riconoscere serie particolari come quelle di Fourier o Taylor, richiedendo un’analisi manuale dettagliata o l’uso di software specifici.

Convergenza serie online: criteri e strumenti per l’analisi

Definizione di convergenza serie

Calcolatore convergenza serie

Criteri di convergenza

Criterio del rapporto

Criterio della radice

Criterio di Leibniz per serie alternanti

Criterio della convergenza assoluta

Convergenza condizionata e assoluta

Serie di potenze

Raggio di convergenza

Convergenza su intervallo di convergenza

Teorema del confronto per serie

Convergenza uniforme e puntuale

Serie di Fourier

Serie Numeriche

Serie Geometrica

Serie Armonica

Serie a Termini Positivi

Strumenti online per la convergenza serie

Applicazioni della convergenza serie in fisica e ingegneria

Metodi numerici per valutare la convergenza

Problemi comuni e errori nella convergenza serie

Calcolatore media ponderata

Radice quadrata di 64

Calcolatori derivate

Leave a Reply Cancel Reply

Chi siamo

Privacy Policy

Termini di servizio

Cookie policy

Contattaci

CALCOLO.ONLINE