Una calcolatrice numeri complessi è uno strumento matematico avanzato utilizzato per eseguire operazioni su numeri complessi. Questi numeri includono una parte reale e una parte immaginaria, rappresentati generalmente nella forma a + bi, dove a è la parte reale, b è la parte immaginaria, e i è l’unità immaginaria (√-1).
La calcolatrice numeri complessi facilita le operazioni come somma, sottrazione, moltiplicazione e divisione, oltre a funzioni più complesse quali il calcolo di moduli, argomenti e l’elevazione a potenza. È inoltre possibile convertire tra diverse forme di numeri complessi, come la forma algebrica (a + bi), la forma trigonometrica e la forma esponenziale.
| Operazione | Esempio |
|---|---|
| Somma | |
| Sottrazione | |
| Moltiplicazione | |
| Divisione | |
| Modulo | |
| Argomento | |
| Forma esponenziale |
È importante notare che la calcolatrice numeri complessi è diversa da una tradizionale in quanto gestisce l’unità immaginaria, che non ha un equivalente nei numeri reali. Poiché il campo dei numeri complessi ha vasta applicazione in diverse aree scientifiche, questa calcolatrice si rivela uno strumento essenziale per studenti, ingegneri, fisici e altri professionisti. Gli algoritmi matematici implementati consentono calcoli precisi e rapidi, indispensabili in situazioni che richiedono una risoluzione deterministica e velocità di elaborazione elevata.
Calcolatore Numeri Complessi
Operazioni di base
Le operazioni di base con i numeri complessi includono l’addizione, la sottrazione, la moltiplicazione e la divisione. Queste operazioni seguono regole specifiche a causa della presenza della parte reale e immaginaria nei numeri complessi.
Addizione
Per addizionare due numeri complessi, si sommano separatamente le parti reali e le parti immaginarie. Se si hanno ![]() e
e ![]() , la somma sarà
, la somma sarà ![]() .
.
Esempio:
Sottrazione
La sottrazione funziona in modo simile all’addizione, sottraendo separatamente le parti reali e immaginarie. Per ![]() e
e ![]() , il risultato sarà
, il risultato sarà ![]() .
.
Esempio:
Moltiplicazione
Per moltiplicare numeri complessi, si applica la proprietà distributiva e si combinano le parti reali e immaginarie, ricordando che ![]() . Se si moltiplicano
. Se si moltiplicano ![]() e
e ![]() , il prodotto sarà
, il prodotto sarà ![]() , che si semplifica in
, che si semplifica in ![]() .
.
Esempio:
Divisione
La divisione tra numeri complessi richiede la moltiplicazione con il complesso coniugato del denominatore per eliminare la parte immaginaria dalla base. Se si divide ![]() per
per ![]() , si moltiplica numeratore e denominatore per il complesso coniugato del denominatore
, si moltiplica numeratore e denominatore per il complesso coniugato del denominatore ![]() , ottenendo
, ottenendo ![]() .
.
Esempio:
Rappresentazione dei numeri complessi
I numeri complessi possono essere rappresentati in diverse forme matematiche, ciascuna vantaggiosa per specifiche applicazioni. La comprensione di queste rappresentazioni è fondamentale per lavorare efficacemente con i numeri complessi.
Forma algebrica
Un numero complesso in forma algebrica si esprime come ![]() , dove
, dove ![]() e
e ![]() sono numeri reali, e
sono numeri reali, e ![]() è l’unità immaginaria, con la proprietà che
è l’unità immaginaria, con la proprietà che ![]() . La componente
. La componente ![]() è detta parte reale, mentre la componente
è detta parte reale, mentre la componente ![]() è nota come parte immaginaria. Un esempio può essere
è nota come parte immaginaria. Un esempio può essere ![]() .
.
Forma trigonometrica
La forma trigonometrica di un numero complesso è data dall’espressione ![]() , dove
, dove ![]() rappresenta il modulo del numero complesso e
rappresenta il modulo del numero complesso e ![]() l’argomento. Questa rappresentazione è utile per la moltiplicazione e la divisione dei numeri complessi.
l’argomento. Questa rappresentazione è utile per la moltiplicazione e la divisione dei numeri complessi.
- Modulo
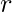 : la distanza dal punto all’origine nel piano complesso.
: la distanza dal punto all’origine nel piano complesso. - Argomento
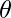 : l’angolo tra la linea che collega il punto all’origine e l’asse reale positivo.
: l’angolo tra la linea che collega il punto all’origine e l’asse reale positivo.
Forma esponenziale
La forma esponenziale di un numero complesso utilizza la formula di Eulero ![]() e si esprime come
e si esprime come ![]() . In questa rappresentazione,
. In questa rappresentazione, ![]() è nuovamente il modulo mentre
è nuovamente il modulo mentre ![]() rappresenta la base dei logaritmi naturali e
rappresenta la base dei logaritmi naturali e ![]() l’argomento del numero complesso. La forma esponenziale semplifica l’elevamento a potenza dei numeri complessi.
l’argomento del numero complesso. La forma esponenziale semplifica l’elevamento a potenza dei numeri complessi.
Conversione tra forme
Nello studio dei numeri complessi, la conversione tra diverse forme rappresentative è un’operazione fondamentale. Un numero complesso può essere rappresentato come forma cartesiana o forma polare.
La forma cartesiana di un numero complesso è espressa come:
![]()
dove ![]() e
e ![]() sono numeri reali, e
sono numeri reali, e ![]() è l’unità immaginaria soddisfacente l’equazione
è l’unità immaginaria soddisfacente l’equazione ![]() .
.
La forma polare di un numero complesso si scrive come:
![]()
o equivalentemente,
![]()
dove ![]() è il modulo del numero complesso e rappresenta la sua distanza dall’origine nel piano complesso, mentre
è il modulo del numero complesso e rappresenta la sua distanza dall’origine nel piano complesso, mentre ![]() è l’argomento, ossia l’angolo formato dal numero complesso con l’asse reale positivo.
è l’argomento, ossia l’angolo formato dal numero complesso con l’asse reale positivo.
Per convertire da cartesiano a polare si utilizzano le seguenti relazioni:
Dove ![]() è una funzione matematica che restituisce l’argomento del punto
è una funzione matematica che restituisce l’argomento del punto ![]() , tenendo conto del segno di entrambe le componenti per determinare il quadrante corretto.
, tenendo conto del segno di entrambe le componenti per determinare il quadrante corretto.
La conversione inversa da polare a cartesiano implica l’uso delle formule:
Queste conversioni permettono di passare con facilità da una rappresentazione all’altra, facilitando operazioni come moltiplicazione e divisione che sono più dirette in forma polare, mentre l’addizione e la sottrazione risultano più semplici in forma cartesiana.
Funzioni complesse essenziali
Nel campo dei numeri complessi, le funzioni complesse essenziali comprendono il coniugato, il modulo e l’argomento. Queste funzioni sono fondamentali per svolgere operazioni complesse e comprendere la natura dei numeri complessi.
Coniugato
Il coniugato di un numero complesso è ottenuto invertendo il segno della parte immaginaria del numero. Se si ha un numero complesso ![]() , dove
, dove ![]() e
e ![]() sono numeri reali e
sono numeri reali e ![]() è l’unità immaginaria, il suo coniugato è
è l’unità immaginaria, il suo coniugato è ![]() .
.
Modulo
Il modulo di un numero complesso, indicato come ![]() , è il valore che rappresenta la distanza del punto associato al numero complesso dall’origine nel piano complesso. Per il numero complesso
, è il valore che rappresenta la distanza del punto associato al numero complesso dall’origine nel piano complesso. Per il numero complesso ![]() , il modulo si calcola come
, il modulo si calcola come ![]() .
.
Argomento
L’argomento di un numero complesso è l’angolo formato dal raggio vettore del numero complesso rispetto all’asse reale positivo nel piano complesso, misurato in radianti. Per ![]() non nullo, l’argomento, indicato come
non nullo, l’argomento, indicato come ![]() , è definito come l’angolo
, è definito come l’angolo ![]() tale che
tale che ![]() , e si determina tramite l’uso di funzioni trigonometriche inverse.
, e si determina tramite l’uso di funzioni trigonometriche inverse.
Potenze e radici
Nel contesto dei numeri complessi, le potenze vengono calcolate utilizzando la formula di De Moivre. Se un numero complesso è espresso sotto forma di numero polare ![]() , la sua potenza
, la sua potenza ![]() -esima è data da:
-esima è data da:
![]()
Dove ![]() è un intero positivo, e
è un intero positivo, e ![]() è l’unità immaginaria.
è l’unità immaginaria.
Per le radici n-esime di un numero complesso ![]() , si applicano le formule:
, si applicano le formule:
![]()
con ![]() che varia da 0 a
che varia da 0 a ![]() . Questo produrrà
. Questo produrrà ![]() radici distinte in quanto il valore di
radici distinte in quanto il valore di ![]() produce angoli differenti.
produce angoli differenti.
Una tabella per visualizzare l’effetto di ![]() sul calcolo delle radici può essere:
sul calcolo delle radici può essere:
| Angolo | |
|---|---|
| 0 | |
| 1 | |
| … | … |
Ogni valore di ![]() corrisponde a una radice distinta nel piano complesso.
corrisponde a una radice distinta nel piano complesso.
Inoltre, è possibile visualizzare le potenze e le radici dei numeri complessi utilizzando un diagramma di Argand, che rappresenta il piano complesso con l’asse reale e l’asse immaginario. Un numero complesso elevato alla ![]() -esima potenza si estenderà radialmente dalla sua posizione iniziale, mentre le
-esima potenza si estenderà radialmente dalla sua posizione iniziale, mentre le ![]() -esime radici saranno disposte simmetricamente rispetto all’origine, formando i vertici di un poligono regolare.
-esime radici saranno disposte simmetricamente rispetto all’origine, formando i vertici di un poligono regolare.
Equazioni con numeri complessi
I numeri complessi si presentano nella forma ![]() , dove
, dove ![]() è la parte reale e
è la parte reale e ![]() la parte immaginaria, e
la parte immaginaria, e ![]() rappresenta l’unità immaginaria tale che
rappresenta l’unità immaginaria tale che ![]() . Nelle equazioni che coinvolgono numeri complessi, si usano metodi algebrici per trovare soluzioni che possiedono sia una componente reale che una immaginaria.
. Nelle equazioni che coinvolgono numeri complessi, si usano metodi algebrici per trovare soluzioni che possiedono sia una componente reale che una immaginaria.
Soluzione di Equazioni Lineari: Un’equazione lineare con numeri complessi segue la forma ![]() , dove
, dove ![]() e
e ![]() sono numeri complessi e
sono numeri complessi e ![]() è l’incognita. Per trovare
è l’incognita. Per trovare ![]() , la formula è
, la formula è ![]() .
.
Equazioni Quadratiche: Le equazioni di secondo grado prevedono una soluzione mediante la formula:
![]()
Dove ![]() ,
, ![]() , e
, e ![]() sono numeri complessi. La discriminante
sono numeri complessi. La discriminante ![]() determina la natura delle radici.
determina la natura delle radici.
- Se la discriminante è positiva, si hanno due soluzioni reali distinte.
- Se la discriminante è zero, si ha una soluzione reale doppia.
- Se la discriminante è negativa, si hanno due soluzioni complesse coniugate.
Radici n-esime: Le radici n-esime di un numero complesso si trovano sfruttando la formula di De Moivre:
![]()
dove ![]() è il modulo del numero complesso,
è il modulo del numero complesso, ![]() è l’argomento principale,
è l’argomento principale, ![]() è il grado della radice, e
è il grado della radice, e ![]() varia da 0 a
varia da 0 a ![]() .
.
La risoluzione di equazioni con numeri complessi si avvale di strumenti come la mappatura su piano di Argand-Gauss e l’utilizzo di software di calcolo simbolico al fine di facilitare le operazioni.
Utilizzo nella fisica
Le calcolatrici di numeri complessi trovano importanti applicazioni nel campo della fisica, specialmente nell’analisi di circuiti elettronici e nella meccanica quantistica, permettendo di gestire grandezze che includono sia una componente reale che una immaginaria.
Impedenza in elettrotecnica
In elettrotecnica, l’impedenza rappresenta una generalizzazione della nozione di resistenza e può essere espressa tramite un numero complesso. Z indica l’impedenza e si articola in una parte reale che rappresenta la resistenza (R) e una parte immaginaria che rappresenta la reattanza (X), con Z = R + jX, dove j è l’unità immaginaria.
- Resistenza (R): Componente che dissipa energia sotto forma di calore.
- Reattanza (X): Componente legata all’accumulo di energia, può essere capacitiva (-jXC) o induttiva (+jXL).
L’impedenza gioca un ruolo cruciale nell’analisi della risposta dei circuiti alle correnti alternative (AC).
Meccanica Quantistica
La meccanica quantistica utilizza numeri complessi per descrivere lo stato quantistico di un sistema. La funzione d’onda Ψ, che rappresenta la distribuzione di probabilità della posizione e del momento di una particella, è in generale un numero complesso. La probabilità di trovare una particella in una certa regione dello spazio è data dal modulo quadro della funzione d’onda, ![]() .
.
- Funzione d’onda (Ψ): Elemento fondamentale che descrive lo stato di un sistema quantistico.
- Modulo quadro (|Ψ|^2): Determina la probabilità di presenza di una particella.
Le calcolatrici di numeri complessi sono strumenti essenziali per analizzare e manipolare queste funzioni d’onda.
Software di calcolo numerico complesso
I software di calcolo numerico complesso sono strumenti informatici progettati per elaborare e manipolare numeri complessi. Questi programmi offrono diverse funzionalità che possono includere l’addizione, la sottrazione, la moltiplicazione, la divisione, l’elevazione a potenza e l’estrazione di radici di numeri complessi. Alcuni software possono anche fornire grafici dei numeri complessi su piani argandiani e supportare la trasformata di Fourier.
Un esempio noto è MATLAB, un ambiente di programmazione avanzato che include funzioni specifiche per i numeri complessi. Un altro software è Mathematica, ampiamente utilizzato per calcoli scientifici e ingegneristici, che supporta operazioni complesse e visualizzazione grafica.
Di seguito è riportata una breve tabella che elenca alcuni dei principali software di calcolo numerico complesso e le loro funzionalità principali:
| Software | Operazioni di base | Visualizzazione Grafica | Altre Funzionalità |
|---|---|---|---|
| MATLAB | Sì | Sì | Toolbox specializzati |
| Mathematica | Sì | Sì | Linguaggio di programmazione |
| Python | Sì | Dipende dalle librerie | Ampio supporto della comunità |
Python, in particolare, diventa un potente strumento per il calcolo numerico complesso quando viene impiegato insieme a librerie come NumPy.
Gli utenti possono scegliere il software più adatto in base alle necessità specifiche del loro lavoro o studio. La scelta dipende dai requisiti di potenza computazionale, facilità d’uso, accessibilità, e dalla possibilità di integrarsi con altri strumenti o sistemi.
Calcolatrici numeriche complesse online
Una calcolatrice numerica complessa online è uno strumento che permette di eseguire operazioni matematiche sui numeri complessi direttamente tramite un browser web. Un numero complesso è una coppia ordinata di numeri reali, scritta nella forma a + bi, dove a rappresenta la parte reale e bi la parte immaginaria. Qui, l’unità immaginaria i soddisfa la condizione ![]() .
.
Questi strumenti sono progettati per facilitare il calcolo di:
- Somma e sottrazione
- Moltiplicazione e divisione
- Modulo e argomento
- Conversione tra la forma algebrica e altre rappresentazioni come quella trigonometrica o esponenziale
Ecco una tabella che illustra alcune funzioni comuni di una calcolatrice complessa online:
| Funzione | Descrizione |
|---|---|
| Operazioni di base | Consente la somma, sottrazione, moltiplicazione e divisione tra numeri complessi. |
| Modulo | Calcola la distanza del numero complesso dall’origine nel piano complesso. |
| Argomento | Determina l’angolo formato dal numero complesso rispetto all’asse reale. |
| Conversione di forma | Trasforma un numero complesso dalla forma algebrica a quella trigonometrica o esponenziale e viceversa. |
Inoltre, molte calcolatrici offrono funzionalità avanzate come l’elevazione a potenza, il calcolo delle radici n-esime, nonché funzioni esponenziali e logaritmiche. La facilità d’uso e l’accessibilità rendono le calcolatrici numeriche complesse online strumenti utili sia per studenti che per professionisti che lavorano con la matematica avanzata.
Educazione e risorse didattiche
In ambito educativo, gli insegnanti spesso incorporano nell’insegnamento delle scienze matematiche l’utilizzo delle calcolatrici per numeri complessi. Questi dispositivi o software sono fondamentali per facilitare la comprensione degli studenti riguardo concetti quali l’algebra complessa e le operazioni con numeri complessi. Le calcolatrici per numeri complessi consentono agli utenti di effettuare calcoli che includono le componenti reali e immaginarie dei numeri complessi.
Ecco alcune risorse didattiche comunemente utilizzate:
- Libri di testo: Offrono concetti teorici e esercizi pratici riguardanti i numeri complessi.
- Software educativi: Forniscono un approccio interattivo all’apprendimento dei numeri complessi.
- Video lezioni: Disponibili su piattaforme online, illustrano passo dopo passo i metodi di risoluzione dei problemi.
- Siti specializzati in matematica: Contengono una vasta gamma di esercizi, esempi guidati e quiz interattivi.
Tabella con esempi di risorse online:
| Risorsa | Tipo di contenuto | Disponibilità |
|---|---|---|
| GeoGebra | Software | Gratuito |
| Khan Academy | Video lezioni | Gratuito |
| Wolfram Alpha | Strumenti di calcolo | Parziale gratuito |
Le università e i college offrono spesso corsi specializzati che incorporano l’uso di calcolatrici complesse, consentendo agli studenti di applicare la teoria all’analisi di circuiti elettrici, fisica quantistica, e ingegneria. Gli educatori incoraggiano l’uso di queste tecnologie per aumentare la comprensione e la capacità analitica degli studenti.
Problematiche comuni e soluzioni
Quando si utilizza una calcolatrice di numeri complessi, gli utenti possono incontrare alcune difficoltà comuni. Di seguito sono elencate alcune di queste problematiche e le relative soluzioni.
Comprensione dell’input:
Gli utenti possono avere difficoltà nell’inserire correttamente i numeri complessi. Le calcolatrici richiedono tipicamente che i numeri complessi siano inseriti in forma algebrica (a + bi), dove a è la parte reale e b è la parte immaginaria, accompagnata dall’unità immaginaria i.
Soluzione:
Utilizzare un esempio rappresentativo per illustrare la corretta forma di input:
| Forma corretta | Input accettato |
|---|---|
| Numeri complessi | |
| Parte reale | |
| Parte immaginaria |
Interpretazione dei risultati:
I risultati possono risultare confusi se gli utenti non sono familiari con le diverse rappresentazioni dei numeri complessi (forma algebrica, forma polare, forma esponenziale).
Soluzione:
Fornire una breve guida alle diverse forme:
- Forma algebrica:
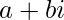
- Forma polare:
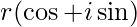 o
o 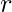
- Forma esponenziale:
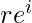
dove ![]() è il modulo e
è il modulo e ![]() è l’argomento del numero complesso.
è l’argomento del numero complesso.
Errori di calcolo:
Errori come l’immissione di un segno errato o la confusione tra ![]() e altre variabili possono condurre a risultati incorretti.
e altre variabili possono condurre a risultati incorretti.
Soluzione:
Doppio controllo degli input e revisione dei risultati in passaggi intermedi.
Limitazioni della calcolatrice:
Alcune calcolatrici non supportano funzioni complesse avanzate come quelle trigonometriche, esponenziali o logaritmiche.
Soluzione:
Verificare le specifiche del dispositivo prima dell’acquisto oppure ricorrere a software di calcolo numerico che supporti operazioni avanzate con i numeri complessi.
L’utilizzo di una calcolatrice numeri complessi richiede attenzione e pratica. Seguendo le soluzioni indicate, gli utenti possono migliorare la propria esperienza nell’uso di tali strumenti matematici.