Un calcolatore integrale è uno strumento digitale utilizzato per computare l’integrale definito o indefinito di una funzione. Gli studenti e i professionisti nel campo delle matematiche utilizzano spesso questi strumenti per semplificare e accelerare i calcoli complessi.

Funzioni principali:

• Calcolo dell’integrale indefinito (antiderivata): Trova la funzione 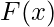il cui tasso di variazione è dato dalla funzione .
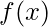• Calcolo dell’integrale definito: Stima l’area sotto la curva di una funzione 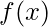tra due punti, 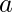e .

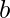Funzione	Descrizione
Integrale indefinito	Trova la funzione originale data la sua derivata
Integrale definito	Calcola l’area sotto la curva in un intervallo specifico

I calcolatori integrali moderni possono affrontare funzioni complesse e permettono agli utenti di specificare le variabili rispetto alle quali integrare. Questi strumenti offrono una gamma di metodi numerici e algoritmici, come la regola del trapezio e la formula di Simpson, per il calcolo dell’integrale definito.

Vantaggi:

• Velocità: Riducono significativamente il tempo necessario per i calcoli.
• Accuratezza: Diminuiscono la possibilità di errore umano.
• Funzionalità: Supportano una vasta gamma di funzioni.

Considerazioni:

• La precisione dipende dal metodo numerico utilizzato e dalla complessità della funzione.
• Non sostituiscono la comprensione concettuale del calcolo integrale.

La familiarizzazione con un calcolatore integrale richiede solitamente la conoscenza di base dei concetti di integrazione e della terminologia matematica associata.

Tipi di integrali

In matematica, gli integrali rappresentano un concetto fondamentale del calcolo infinitesimale. Si distinguono principalmente in tre categorie: gli integrali definiti, che calcolano l’area sotto una curva; gli integrali indefiniti, che rappresentano antiderivate di una funzione; e gli integrali impropri, che estendono il concetto di integrazione a limiti più ampi.

Integrali definiti

Un integrale definito calcola l’area compresa tra l’asse delle ascisse e la curva di una funzione reale in un intervallo chiuso . La notazione standard dell’integrale definito è la seguente:

   

dove è la funzione da integrare, e sono gli estremi di integrazione e indica che l’integrazione è rispetto alla variabile .

Integrali indefiniti

Gli integrali indefiniti, conosciuti anche come antiderivate, sono funzioni che descrivono una famiglia di funzioni la cui derivata è la funzione originale. Non sono legati a intervalli specifici e vengono rappresentati come:

   

In questa espressione, è una funzione tale che , e è una costante di integrazione che rappresenta l’infinità di antiderivate correlate a .

Integrali impropri

Gli integrali impropri si riferiscono ad integrali definiti con almeno un estremo di integrazione infinito o una funzione integranda che presenta una discontinuità infinita. Sono espressi come:

   

in cui almeno uno tra e tende a o , oppure:

   

dove ha una discontinuità infinita in . In questi casi, si utilizzano i limiti per valutare l’integrale in modo corretto.

Metodi di integrazione

L'integrazione è un concetto fondamentale dell'analisi matematica e si suddivide in vari metodi specifici per affrontare diverse tipologie di funzioni.

Integrazione per parti

L'integrazione per parti è una tecnica che si basa sulla formula di derivazione del prodotto di due funzioni. Si applica quando l'integrando è il prodotto di due funzioni, una delle quali si integra facilmente mentre l'altra si deriva facilmente.

Formula: 

Sostituzione

La sostituzione, nota anche come cambio di variabile, è utilizzata per semplificare l'integrazione attraverso la trasformazione dell'integrando in una forma più gestibile.

Esempio: Se si ha , si può porre , quindi .

Frazioni parziali

L'integrazione mediante frazioni parziali si utilizza quando l'integrando è una frazione razionale. Si scompone la frazione in un insieme di frazioni più semplici, che possono essere integrate individualmente.

Passaggi:

1. Fattorizzare il denominatore.
2. Esprimere l'integrando come somma di frazioni con denominatori lineari o quadratici.
3. Integrare ciascuna frazione separatamente.

Integrazione numerica

L'integrazione numerica si riferisce a metodi approssimativi per calcolare il valore di un integrale quando non è possibile una soluzione analitica. Ciò è comune per funzioni complesse o dati empirici.

Metodi comuni:

• Regola del trapezio
• Regola di Simpson
• Integrazione di Monte Carlo

Tabella dei metodi numerici:

Metodo	Descrizione
Regola del trapezio	Approssima l'area sotto la curva con trapezi
Regola di Simpson	Utilizza parabole per una stima più accurata
Monte Carlo	Applica la statistica per valutare l'integrale

Software e strumenti online

Esistono diversi software e strumenti online che consentono di effettuare il calcolo degli integrali. Questi programmi sono generalmente utilizzati da studenti e professionisti per risolvere complessi problemi matematici nel campo del calcolo differenziale e integrale.

Wolfram Alpha: Si tratta di un motore di calcolo simbolico avanzato, che permette di calcolare integrali definiti e indefiniti. Offre una vasta gamma di funzionalità, inclusa la possibilità di visualizzare grafici.

Strumento	Tipo di integrali	Caratteristiche
Wolfram Alpha	Definiti e indefiniti	Visualizzazione grafici
Symbolab	Definiti e indefiniti	Passi di calcolo spiegati
GeoGebra	Definiti e indefiniti	Strumenti interattivi

Symbolab: Questo strumento online, oltre a calcolare gli integrali, fornisce passo dopo passo le spiegazioni dei procedimenti utilizzati, rendendo più semplice la comprensione delle operazioni matematiche.

GeoGebra: È una piattaforma educativa che offre molti strumenti, tra cui il calcolo integrale. Permette di eseguire operazioni in modo interattivo e di esplorare graficamente le funzioni matematiche.

Altri strumenti online possono includere calcolatori più semplici, come quelli offerti da siti web educativi, che forniscono risultati rapidi ma potrebbero non avere la profondità o la flessibilità di Wolfram Alpha o Symbolab. L'utente deve scegliere lo strumento adatto in base al livello di complessità del problema da risolvere e alle proprie esigenze educative.

Calcolatori integrali grafici

I calcolatori integrali grafici sono strumenti software utilizzati per calcolare l'area sotto la curva di una funzione, che matematicamente rappresenta l'integrazione. Questi strumenti sono particolarmente utili per gli studenti e i professionisti che richiedono una rappresentazione visiva dell'integrale.

Caratteristiche principali:

• Interfaccia utente: Offre una piattaforma interattiva che permette di inserire la funzione desiderata.
• Visualizzazione grafica: Mostra il grafico della funzione e l’area sottesa, facilitando la comprensione dell'integrale definito.
• Funzioni supportate: In grado di gestire una vasta gamma di funzioni, tra cui polinomiali, trigonometriche e logaritmiche.

Funzionalità avanzate:

• Limiti di integrazione: Permettono di specificare gli intervalli sui quali calcolare l'integrale.
• Risultati numerici e simbolici: Forniscono il valore dell'integrale in forma numerica o come espressione simbolica.

Applicazioni Pratiche dei Calcolatori Integrali

I calcolatori integrali sono strumenti fondamentali in vari ambiti scientifici e tecnologici. Essi consentono la risoluzione di problemi complessi legati all'analisi matematica e alle sue applicazioni pratiche.

Ingegneria

In ambito ingegneristico, i calcolatori integrali permettono l'analisi e la progettazione di componenti e sistemi.

Un esempio specifico è il calcolo dell'area di sezione trasversale dei materiali, cruciale per determinare la resistenza e la stabilità nelle costruzioni ingegneristiche.

La loro applicabilità si estende anche al calcolo di carichi fluidodinamici in ambito aerospaziale e alla progettazione di circuiti in ingegneria elettrica.

• Calcolo dell'Area: Stabilità strutturale
• Fluidodinamica: Progettazione aerospaziale
• Circuiti Elettrici: Analisi di corrente e tensione

Fisica

I calcolatori integrali in fisica sono impiegati per risolvere equazioni che descrivono fenomeni fisici.

Essi sono utilizzati nel calcolo del lavoro svolto dalle forze o nel calcolo di grandezze fisiche come campo magnetico e elettrico.

In ottica, sono strumentali nel definire le proprietà delle lenti attraverso l'integrazione della luce rifratta.

• Lavoro delle Forze: Energia meccanica
• Campi Magnetici ed Elettrici: Intensità e distribuzione
• Ottica: Proprietà delle lenti

Economia

In economia, i calcolatori integrali forniscono analisi precise per modelli economici e finanziari.

Essi sono utilizzati per prevedere la crescita del mercato attraverso l'integrazione delle curve di domanda e offerta.

Altro impiego rilevante è il calcolo delle aree sotto la curva delle funzioni di costo e beneficio, determinante nell'analisi delle performance aziendali.

• Curve di Domanda e Offerta: Previsioni di mercato
• Funzioni di Costo e Beneficio: Valutazione delle performance aziendali

Integrazione simbolica e numerica

L'integrazione simbolica si riferisce al processo di calcolo dell'integrale di una funzione in forma chiusa. In altre parole, si cerca una funzione primitiva espressa attraverso simboli matematici standard.

Gli integrazione simbolica è spesso gestita da software di algebra computerizzata come Mathematica o Maple, che forniscono soluzioni esatte, se possibile.

D'altro canto, l'integrazione numerica consiste nel calcolare un'approssimazione dell'integrale di una funzione. Questo avviene quando non si può integrare una funzione simbolicamente o quando si richiede solo una stima numerica.

Questa viene eseguita attraverso metodi come la regola dei trapezi o il metodo di Simpson.

Ecco una tabella che evidenzia le differenze principali:

Caratteristica	Integrazione Simbolica	Integrazione Numerica
Tipo di Risultato	Esatto	Approssimato
Strumenti Software	Algebra computerizzata	Metodi numerici
Metodi Utilizzati	Riscrittura simbolica	Discretizzazione e approssimazione

Questi metodi integrativi sono fondamentali in vari campi scientifici e ingegneristici. Questi campi hanno la necessità di determinare aree sotto curve, costanti di proporzionalità e altri valori che sono il risultato di processi di integrazione continua.

Nella scelta tra integrazione simbolica e numerica, gli utenti devono valutare la complessità della funzione, la possibilità di ottenere una forma chiusa e la precisione richiesta.

In molti casi, l'integrazione numerica è preferibile a causa della sua flessibilità e dell'alta probabilità di poter gestire funzioni complesse con integrale non esprimibile in forma chiusa.

Limiti e Accuratezza dei Calcolatori Integrali

I calcolatori integrali sono strumenti software che automatizzano il processo del calcolo degli integrali, un'operazione fondamentale nel campo della matematica e dell'ingegneria. Nonostante siano di grande aiuto, presentano alcuni limiti e fluttuazioni nell'accuratezza che occorre considerare.

Precisione Numerica: I calcolatori integrali si basano su algoritmi numerici che approssimano il valore degli integrali. L'accuratezza dei risultati dipende dalla precisione dell'algoritmo utilizzato.

• Metodi Numerici: Alcuni dei metodi più noti includono la regola dei trapezi e il metodo di Simpson.
• Errore Numerico: Piccole differenze possono sorgere a causa dell'arrotondamento numerico.

Limiti di Calcolo: La complessità di alcune funzioni può superare le capacità dei calcolatori integrali.

Funzioni con discontinuità, singolarità o comportamenti oscillatori estremi possono risultare difficili da integrare con precisione.

Conoscenze Pregresse: La corretta configurazione dei parametri del calcolatore è essenziale per ottenere risultati affidabili. L'utente deve avere una conoscenza di base della funzione che sta integrando.

Tabella di Confronto: Risultati Tipici vs. Calcolatori Integrali

Tipo di Funzione	Risultato Tipico	Calcolatore Integrale
Polinomiale	Alta precisione	Risultato affidabile
Oscillante	Possibile imprecisione	Dipende dall'algoritmo
Con singolarità	Errore elevato	Potenzialmente inesatto

Tutorial e Guide di Utilizzo

Per utilizzare un calcolatore di integrali, è essenziale comprendere i passaggi di base. Di seguito è riportata una guida step-by-step:

1. Selezione della funzione: Inizialmente, l'utente deve inserire la funzione matematica che desidera integrare. La funzione deve essere inserita nell'apposito campo, rispettando la sintassi richiesta dal calcolatore.
2. Definizione degli intervalli: Se si esegue un'integrazione definita, specificare gli estremi di integrazione, ovvero i valori iniziale e finale dell'intervallo su cui si calcola l'integrale.
3. Scelta del metodo: Scegliere il metodo di integrazione, se l'opzione è disponibile. Alcuni calcolatori supportano diversi metodi, come l'integrazione numerica o simbolica.
4. Calcolo: Una volta inseriti tutti i dati, selezionare l'opzione per calcolare l'integrale. Attendere che il processo si completi per vedere il risultato.
5. Interpretazione dei risultati: Il risultato sarà visualizzato sullo schermo. Se l'integrale è definito, il risultato sarà un numero che rappresenta l'area sotto la curva della funzione nell'intervallo specificato.

Nota Bene: Verificare sempre la correttezza della funzione inserita e degli intervalli di integrazione prima di procedere con il calcolo.

Passaggio	Descrizione
Selezione della funzione	Inserire la funzione secondo la sintassi del calcolatore.
Definizione degli intervalli	Indicare gli estremi di integrazione per integrali definiti.
Scelta del metodo	Optare per il metodo di integrazione preferito, se disponibile.
Calcolo	Avviare il processo di calcolo.
Interpretazione dei risultati	Analizzare il numero risultante come area sotto la funzione o come integrale indefinito.

Si raccomanda di consultare la documentazione o le FAQ del calcolatore per assistenza su problemi specifici o errori.

Problemi comuni e risoluzione

Quando si utilizza un calcolatore di integrali, gli utenti possono incontrare alcuni problemi frequenti.

Di seguito una tabella dei problemi più comuni e delle relative soluzioni:

Problema	Soluzione
Errore di sintassi	Verificare che la funzione sia inserita correttamente.	Rispettare la notazione matematica standard ed evitare errori di battitura.
Limiti d'integrazione mancanti	Assicurarsi di specificare i limiti superiori e inferiori dell'integrale.
Funzione non integrabile	Controllare che la funzione sia integrabile nel dominio specificato.	Se necessario, consultare materiale di riferimento per confermare.
Tempo di elaborazione eccessivo	Ridurre la complessità della funzione o aumentare le risorse di calcolo se possibile.

Inoltre, l'utente può seguire questi passaggi per risolvere problemi meno specifici:

1. Rilettura: Talvolta, rileggere la funzione inserita può aiutare a identificare errori non immediatamente evidenti.
2. Controllo dei parametri: Assicurarsi che tutti i parametri e le variabili siano definiti correttamente.
3. Semplificazione: Se possibile, semplificare matematicamente l'espressione prima di inserirla nel calcolatore.

Alcuni integrali possono non avere soluzioni in forma chiusa e potrebbero richiedere metodi di integrazione numerica anziché analitica. In tali casi, è consigliabile utilizzare un software adeguato o consultare testi avanzati di matematica.

Novità e aggiornamenti nel software di integrazione

Negli ultimi mesi, i software di calcolo integrale hanno registrato miglioramenti significativi.

Questi aggiornamenti mirano a ottimizzare le performance e ampliare le funzionalità disponibili per gli utenti.

Velocità di Calcolo Migliorata:

• Gli algoritmi sono stati affinati per consentire un calcolo più rapido delle integrali.
• Ora il software supporta anche CPU multicore e GPU, accelerando la computazione paralella.

Interfaccia Utente Rinnovata:

• La nuova interfaccia ha un disegno più pulito e intuitivo.
• Inoltre, è stata migliorata la disposizione degli elementi per facilitare la navigazione.

Precisone e Accuratezza:

• Sono stati introdotti nuovi metodi numerici per aumentare la precisione dei calcoli.
• Anche il software ha corretto errori noti e migliorato l’algoritmo di approssimazione.

Funzionalità Aggiuntive:

• Ora il software supporta anche il calcolo simbolico, per manipolare espressioni integrali e ottenere risultati in forma esatta.
• Inoltre, sono state aggiunte funzioni di visualizzazione grafica avanzate per una rappresentazione immediata delle aree sottese alla curva.

Sono inoltre stati implementati nuovi moduli per rendere il software compatibile con sistemi operativi aggiornati e dispositivi mobile, permettendo così agli utenti di utilizzare queste risorse in mobilità.

Infine, è stata potenziata l’assistenza utente con l’aggiunta di guide dettagliate e una sezione FAQ arricchita, assicurando una risorsa completa per la soluzione di possibili dubbi o problemi riscontrati dall’utente.