Il calcolo differenziale è un ramo fondamentale dell’analisi matematica. Si occupa dello studio delle derivate e dei loro molteplici utilizzi.
Una derivata di una funzione in un punto può essere intuitivamente compresa come la pendenza della tangente alla curva della funzione in quel punto. Matematicamente, essa rappresenta il tasso istantaneo di variazione della funzione rispetto alla variabile indipendente.
Per esemplificare, si consideri la funzione ![]() :
:
| | |
|---|---|
| 1 | a |
| 2 | b |
| 3 | c |
| 4 | d |
| 5 | e |
La derivata di ![]() in
in ![]() =2, indicata come
=2, indicata come ![]() , misura quanto velocemente il valore di
, misura quanto velocemente il valore di ![]() cambia all’aumentare di
cambia all’aumentare di ![]() in
in ![]() =2.
=2.
Calcolatore Derivata
Concetti chiave del calcolo differenziale:
- Limite: Il limite è il fondamento del calcolo delle derivate. Esso indica il valore che una funzione si avvicina man mano che l’input si avvicina a un certo punto.
- Continuità: La continuità è una proprietà necessaria affinché la derivata in un punto sia definita. Una funzione è continua se non ci sono salti, spaccature o asintoti nella sua curva.
- Differenziabilità: Una funzione è differenziabile in un punto se esiste la sua derivata in quel punto. Ne consegue che è anche continua in quel punto.
Fondamenti di Derivate
Nell’analisi matematica, le derivate sono lo strumento fondamentale per studiare il tasso di variazione di una funzione. Esse sono indispensabili in vari campi come fisica, ingegneria e economia.
Definizione di Derivata
La derivata di una funzione in un punto è il tasso al quale il valore della funzione cambia rispetto a una variazione dell’input. Formalmente, se ![]() è una funzione e
è una funzione e ![]() è un punto nell’intervallo di
è un punto nell’intervallo di ![]() , la derivata di
, la derivata di ![]() in
in ![]() è definita come il limite, se esiste, del rapporto incrementale:
è definita come il limite, se esiste, del rapporto incrementale:
![]()
Limiti e Continuità
Il concetto di limite è vitale nello studio delle derivate. Un limite descrive il comportamento di una funzione man mano che l’input si avvicina a un certo valore. Per definire la derivata, è necessario che il limite del rapporto incrementale esista.
Una funzione ![]() è continua in un punto
è continua in un punto ![]() se:
se:
-
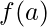 è definita,
è definita, - Il limite di
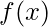 per
per 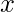 che tende ad
che tende ad 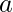 esiste,
esiste, - Il limite di
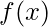 per
per 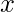 che tende ad
che tende ad 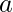 è uguale a
è uguale a 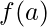 .
.
Teorema del Limite Centrale
Nonostante il nome possa trarre in inganno, il Teorema del Limite Centrale non si applica direttamente alla teoria delle derivate, bensì è un concetto della teoria della probabilità. Pertanto, si consiglia di concentrarsi sui limiti specifici che definiscono le derivate per meglio comprendere i fondamenti di questo strumento dell’analisi matematica.
Regole di Derivazione
Nell’analisi matematica, le regole di derivazione sono cruciali per il calcolo differenziale. Esse forniscono metodi sistematici per determinare la derivata di vari tipi di funzioni, comprese quelle risultanti da combinazioni più complesse.
Regola del Prodotto
La Regola del Prodotto è utilizzata quando si deve derivare il prodotto di due funzioni. Se sono presenti due funzioni differenziabili, ![]() e
e ![]() , la loro derivata sarà:
, la loro derivata sarà:
![]()
Questa formula indica che la derivata del prodotto è la derivata della prima funzione moltiplicata per la seconda funzione più la prima funzione moltiplicata per la derivata della seconda funzione.
Regola del Quoziente
La Regola del Quoziente si applica alla derivata di un quoziente di due funzioni. Dato un quoziente dove ![]() è il numeratore e
è il numeratore e ![]() è il denominatore, la derivata si calcola come segue:
è il denominatore, la derivata si calcola come segue:
![]()
Questa regola indica che la derivata del quoziente è il denominatore moltiplicato per la derivata del numeratore meno il numeratore moltiplicato per la derivata del denominatore, il tutto diviso per il quadrato del denominatore.
Regola della Catena
La Regola della Catena è fondamentale quando una funzione è composta da altre funzioni. Se ![]() , allora la derivata di
, allora la derivata di ![]() rispetto a
rispetto a ![]() è:
è:
![]()
Questo significa che la derivata della funzione composta è il prodotto delle derivate delle funzioni interne.
Derivate delle Funzioni Elementari
Le Derivate delle Funzioni Elementari includono le regole di derivazione per le funzioni base che troviamo in matematica, come potenze, esponenziali e logaritmi. Per esempio:
- La derivata di
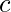 , dove
, dove 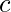 è una costante, è 0.
è una costante, è 0. - La derivata di
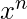 , dove
, dove 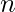 è un numero reale, è
è un numero reale, è 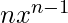 .
. - La derivata di
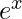 è
è 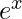 .
. - La derivata del logaritmo naturale
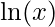 è
è 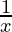 .
.
Applicazioni delle derivate
Le derivate hanno molteplici applicazioni in vari campi della matematica e delle scienze, come lo studio di funzioni, l’ottimizzazione di processi, l’analisi dei grafici e la risoluzione di problemi legati al movimento.
Studio di funzione
Le derivate sono strumentali nello studio di funzioni per determinare i punti critici, ovvero quei valori in cui la funzione presenta massimi, minimi o punti di flesso. Una funzione derivabile ![]() può avere un punto critico in
può avere un punto critico in ![]() se
se ![]() o se la derivata non esiste in quel punto.
o se la derivata non esiste in quel punto.
Ottimizzazione
In economia e ingegneria, le derivate permettono di ottimizzare funzioni che rappresentano costi, ricavi o altri parametri rilevanti. Trovando i punti in cui la derivata prima è zero e analizzando la derivata seconda, si possono identificare i massimi e minimi assoluti per massimizzare l’efficienza o il profitto.
Analisi di grafici
L’analisi delle derivate consente di comprendere la concavità e la convessità di una funzione e di tracciare il suo grafico con maggiore precisione. Analizzando il segno della derivata prima e seconda, è possibile inferire sull’andamento della funzione e i punti di non derivabilità.
Problemi di velocità e accelerazione
In fisica, la derivata prima rappresenta la velocità di un oggetto in movimento, mentre la derivata seconda rappresenta l’accelerazione. Queste possono essere utilizzate, per esempio, per studiare il movimento di un corpo in caduta libera o l’accelerazione di un veicolo.
Derivate parziali
Le derivate parziali rappresentano il tasso di variazione di una funzione rispetto a ciascuna delle variabili indipendenti. Esse sono fondamentali in diversi campi come la matematica, fisica e l’ingegneria.
Funzioni di più variabili
Una funzione di più variabili ![]() dipende da più di una variabile indipendente. Per determinare la derivata parziale di f rispetto alla variabile x, si considerano le altre variabili come costanti e si applica il processo di derivazione rispetto a x. La notazione comune per la derivata parziale di f rispetto a x è ∂f/∂x. Analogamente, ∂f/∂y indica la derivata parziale di f rispetto a y, e così via per le altre variabili.
dipende da più di una variabile indipendente. Per determinare la derivata parziale di f rispetto alla variabile x, si considerano le altre variabili come costanti e si applica il processo di derivazione rispetto a x. La notazione comune per la derivata parziale di f rispetto a x è ∂f/∂x. Analogamente, ∂f/∂y indica la derivata parziale di f rispetto a y, e così via per le altre variabili.
Gradiente e direzionalità
Il gradiente di una funzione ![]() è un vettore che contiene tutte le derivate parziali rispetto alle sue variabili. Viene denotato come grad f o ∇f. Le componenti del gradiente sono
è un vettore che contiene tutte le derivate parziali rispetto alle sue variabili. Viene denotato come grad f o ∇f. Le componenti del gradiente sono ![]() . Il gradiente punta nella direzione di maggiore aumento del valore della funzione.
. Il gradiente punta nella direzione di maggiore aumento del valore della funzione.
La derivata direzionale in un punto in una data direzione è il tasso di variazione della funzione in quella direzione. È calcolata come il prodotto scalare del gradiente con un vettore unitario che indica la direzione considerata.
Metodi di derivazione numerica
La derivazione numerica è l’approccio utilizzato per approssimare le derivate di funzioni che possono non essere facilmente derivabili analiticamente. Questi metodi sono essenziali nell’analisi numerica e nel calcolo scientifico.
- Differenze finite: Questo metodo approssima le derivate utilizzando delle differenze fra i valori della funzione in punti discreti.
- Esempi di formule incluse in questo metodo sono:
- Derivata in avanti:
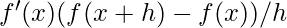
- Derivata all’indietro:
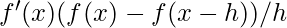
- Derivata centrata:
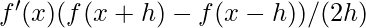
- Derivata in avanti:
Dove h è un piccolo passo nella direzione di x.
- Metodi polinomiali: Questi metodi coinvolgono l’approssimazione della funzione tramite un polinomio e la successiva derivazione di tale polinomio. Il polinomio di Taylor è un esempio comune.
| Metodo | Descrizione |
|---|---|
| Polinomio di Taylor | Trova un polinomio che approssima la funzione intorno a un punto. La derivata è calcolata direttamente dal polinomio. |
| Extrapolazione di Richardson | Migliora la stima delle derivate riducendo l’errore della differenza finita attraverso iterazioni. |
- Metodi spettrali: Questi si basano sulla trasformazione della funzione in un’altra dove è più semplice calcolare le derivate, come per esempio nello spazio di Fourier o con i polinomi di Chebyshev.
La precisione di questi metodi dipende dalla scelta del passo h o dalla natura della funzione. Essi sono spesso implementati in software di calcolo matematico per facilitare l’analisi di funzioni complesse.
Strumenti e tecnologie per il calcolo delle derivate
Nell’ambito del calcolo differenziale, il calcolo delle derivate è fondamentale.
Esistono diversi strumenti e tecnologie utilizzati da studenti, accademici e professionisti per questo compito.
I calcolatori di derivate online sono strumenti accessibili che permettono di ottenere rapidamente le derivate di funzioni matematiche. Questi calcolatori richiedono di inserire la funzione e in seguito forniscono la derivata, a volte anche con i passaggi di calcolo.
Le applicazioni software come Mathematica, MATLAB e Maple sono esempi di tecnologie avanzate per il calcolo simbolico, che includono tra le loro funzioni anche quelle per derivare espressioni matematiche.
Questi software possono gestire funzioni complesse e offrono una varietà di metodi per la manipolazione algebraica, la visualizzazione grafica e l’analisi numerica delle derivate.
Inoltre, i fogli di calcolo come Microsoft Excel possono essere configurati per calcolare derivati numericamente attraverso approcci come le differenze finite.
Un’altra risorsa importante è rappresentata dalle biblioteche software, come SymPy per Python, che forniscono funzionalità di calcolo simbolico e sono particolarmente utili per lo sviluppo di progetti che richiedono calcolo delle derivate in ambiente di programmazione.
| Strumento | Tipo | Caratteristiche Principali |
|---|---|---|
| Calcolatori online | Web-based | Accessibilità, utilizzo immediato senza installazione |
| Mathematica | Software | Calcolo simbolico avanzato, visualizzazione, manipolazione |
| MATLAB | Software | Ampio raggio di funzionalità matematiche e grafiche |
| Maple | Software | Analisi, algebra e calcolo simbolico |
| Excel | Foglio di calcolo | Calcolo numerico tramite formule |
| SymPy | Libreria Software | Integrazione con linguaggi di programmazione, open source |
L’evoluzione tecnologica continua a portare nuovi strumenti e metodi per il calcolo delle derivate, migliorando l’accuratezza e velocizzando i processi di calcolo matematico.
Esercizi di Pratica sulle Derivate
Nello studio del calcolo differenziale, la competenza nell’applicare le derivate è fondamentale. Gli esercizi di pratica sono strumenti essenziali per affinare questa abilità.
Di seguito vengono presentati esempi che possono essere utilizzati per esercitarsi.
Esempio 1: Trova la derivata di ![]() .
.
Soluzione: Utilizzando la regola di potenza, si ottiene ![]() .
.
Esempio 2: Determina la derivata di ![]() .
.
Soluzione: Applicando la regola di potenza a ciascun termine, si ha ![]() .
.
Per consolidare il processo, si può costruire una tabella:
| Funzione | Derivata |
|---|---|
Pratica ulteriore può includere il calcolo di derivate di funzioni più complesse, come quelle che richiedono la regola del prodotto o della catena.
Ad esempio, si può chiedere quale sia la derivata di ![]() o di
o di ![]() .
.
Per facilitare l’apprendimento, ecco alcuni passaggi chiave quando si affrontano esercizi sulle derivate:
- Identificare la regola di derivazione pertinente (regola di potenza, prodotto, quoziente, catena).
- Applicare la regola alla funzione data.
- Semplificare il risultato se necessario.
Errori comuni nel calcolo delle derivate
Nel calcolo delle derivate, gli errori di algebra sono frequenti e possono derivare da una manipolazione scorretta delle espressioni.
Ad esempio, nella derivazione di funzioni composte non applicare correttamente la regola della catena può portare a risultati errati.
Errore nella derivazione delle funzioni trigonometriche: molti studenti sbagliano le derivate di seno e coseno, confondendo le due.
È essenziale ricordare che la derivata di ![]() è
è ![]() e quella di
e quella di ![]() è
è ![]() .
.
Gli studenti talvolta ignorano che le costanti moltiplicative si mantengono invarianti durante la derivazione.
Per esempio, la derivata di ![]() rispetto a
rispetto a ![]() è
è ![]() , non semplicemente
, non semplicemente ![]() .
.
Un altro errore tipico è quello di non rispettare la regola del prodotto quando si derivano funzioni che sono prodotti di altre funzioni.
Questo porta a conclusioni errate come assumere che la derivata di ![]() sia il prodotto delle derivate singole di
sia il prodotto delle derivate singole di ![]() e di
e di ![]() .
.
Le funzioni composte presentano ulteriori sfide:
- Dimenticare di applicare la regola della catena quando si ha a che fare con funzioni annidate (funzioni all’interno di altre funzioni).
- Trascurare la derivata della funzione esterna, concentrando l’attenzione solo su quella interna.
Ecco una tabella riepilogativa degli errori comuni:
| Errore | Esempio Errato | Esempio Corretto |
|---|---|---|
| Algebra | ||
| Funzioni trigonometriche | ||
| Costanti moltiplicative | ||
| Regola del prodotto | ||
| Regola della catena |
Per migliorare, è utile esercitarsi con vari esercizi e verificare ogni passaggio del calcolo confrontandolo con le regole del calcolo differenziale.
Storia del calcolo differenziale
Il calcolo differenziale è un ramo della matematica che si occupa dello studio delle derivate e delle loro applicazioni. Gli albori della sua storia risalgono al XVII secolo.
In quel periodo, matematici come Isaac Newton e Gottfried Wilhelm Leibniz apportarono contributi fondamentali in modo indipendente.
- Isaac Newton sviluppò il concetto di “flussioni”, che oggi conosciamo come derivate, nell’ambito della sua formulazione della legge della gravitazione universale.
- Gottfried Wilhelm Leibniz, d’altra parte, introdusse la notazione ancora oggi utilizzata per denotare il calcolo differenziale, come il simbolo
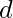 per indicare la derivazione.
per indicare la derivazione.
Seguendo le loro scoperte, si strutturò una disciplina matematica che esamina le variazioni delle funzioni e permette la soluzione di problemi relativi ai tassi di cambiamento e alle pendenze delle curve.
La terminologia “calcolo differenziale” fu diffusa nei lavori di Leonhard Euler, un matematico svizzero del XVIII secolo, che contribuì notevolmente allo sviluppo della teoria.
| Secolo | Matematico | Contributo |
|---|---|---|
| XVII | Isaac Newton | Formulazione delle “flussioni” |
| XVII | G. W. Leibniz | Notazione differenziale e sviluppo teorico |
| XVIII | Leonhard Euler | Sviluppo e divulgazione del calcolo differenziale |
Diverse controversie caratterizzarono la storia del calcolo differenziale. Tra queste, la priorità della scoperta generò dispute tra i sostenitori di Newton e quelli di Leibniz. Nonostante le controversie, tale ramo della matematica si affermò come fondamentale per lo studio e l’analisi di molteplici domini scientifici e tecnologici.
Sviluppi recenti nel calcolo delle derivate
Negli ultimi anni, il campo del calcolo delle derivate ha visto notevoli innovazioni, sia in termini di teoria che di applicazioni pratiche.
La creazione di nuovi algoritmi e l’ottimizzazione di quelli esistenti hanno permesso di aumentare significativamente l’efficienza nel calcolo delle derivate. Questo è particolarmente utile per funzioni complesse o dati di grandi dimensioni.
Tecniche Avanzate:
- Differenziazione Automatica: Metodo computazionale che permette di ottenere derivati di funzioni in modo efficiente e preciso. Attraverso sistemi come i grafici computazionali, il processo di differenziazione può essere completamente automatizzato.
- Algoritmi Basati su Apprendimento Automatico: L’applicazione di tecniche di machine learning al calcolo delle derivate permette di prevedere i modelli dei derivati funzionali con una precisione sempre maggiore.
Software e Strumenti:
- SymPy: Biblioteca Python per matematica simbolica che supporta la differenziazione simbolica.
- TensorFlow e PyTorch: Framework di deep learning che includono la differenziazione automatica per ottimizzare le reti neurali.
In termini di ricerca, lo studio sulle equazioni differenziali stocastiche ha portato a una migliore comprensione delle derivati in ambienti aleatori.
Questo ha implicazioni dirette sia nel campo della finanza che nelle scienze naturali.
Parallelamente, l’introduzione dell’hardware specializzato come le GPU (Graphics Processing Unit) e i TPU (Tensor Processing Unit) ha migliorato notevolmente la velocità dei calcoli.
Questo ha reso possibile il trattamento di complessi problemi di ottimizzazione in tempi molto ridotti.
Questi progressi hanno trovato applicazioni in svariati settori, dalla fisica delle particelle all’ingegneria aerospaziale, dimostrando l’importanza fondamentale delle derivate nel mondo scientifico e ingegneristico.