Calcolatrice trigonometrica triangolo rettangolo
Written by: H. Candido on 2024-06-22
La trigonometria è un ramo della matematica che studia le relazioni tra gli angoli e i lati dei triangoli, in particolare quelli rettangoli. Un triangolo rettangolo è una figura geometrica con un angolo di 90 gradi, chiamato angolo retto, e due angoli acuti. I lati del triangolo rettangolo sono denominati come segue:
- Ipotenusa: il lato più lungo, opposto all’angolo retto.
- Cateto adiacente: il lato che si trova accanto all’angolo di riferimento e forma con l’ipotenusa l’angolo retto.
- Cateto opposto: il lato opposto all’angolo di riferimento.
Le funzioni trigonometriche principali sono il seno (sen), il coseno (cos) e la tangente (tan), che mettono in relazione gli angoli acuti di un triangolo rettangolo con i rapporti dei suoi lati. Queste funzioni sono definite come:
| Funzione | Definizione |
|---|---|
| Seno (sen) | Cateto opposto / Ipotenusa |
| Coseno (cos) | Cateto adiacente / Ipotenusa |
| Tangente (tan) | Cateto opposto / Cateto adiacente |
La calcolatrice trigonometrica per triangoli rettangoli permette di determinare i valori di queste funzioni a partire da un angolo acuto, consentendo di calcolare la lunghezza dei lati mancanti e gli angoli del triangolo. Questo strumento è fondamentale per applicazioni pratiche in vari campi come l’ingegneria, l’architettura, l’aerospaziale e la navigazione.
Trigonometrico triangolo rettangolo
Funzioni trigonometriche di base
Le funzioni trigonometriche di base in un triangolo rettangolo sono il seno, il coseno e la tangente. Ciascuna di queste rapporta le lunghezze dei lati di un triangolo rettangolo agli angoli acuti del triangolo.
Seno
Il seno di un angolo in un triangolo rettangolo si definisce come il rapporto tra la lunghezza del cateto opposto all’angolo e la lunghezza dell’ipotenusa. La formula è la seguente:
- Seno (α) = lunghezza del cateto opposto / lunghezza dell’ipotenusa
Nella tabella qui sotto è possibile vedere esempi dei valori di seno per angoli comuni:
| Angolo (α) | Seno (sin α) |
|---|---|
| 0° | 0 |
| 30° | 1/2 |
| 45° | √2/2 |
| 60° | √3/2 |
| 90° | 1 |
Coseno
Il coseno si calcola come il rapporto tra la lunghezza del cateto adiacente all’angolo considerato e la lunghezza dell’ipotenusa. Ecco la formula rappresentativa:
- Coseno (α) = lunghezza del cateto adiacente / lunghezza dell’ipotenusa
Di seguito, una tabella con i valori di coseno per gli stessi angoli usati in precedenza:
| Angolo (α) | Coseno (cos α) |
|---|---|
| 0° | 1 |
| 30° | √3/2 |
| 45° | √2/2 |
| 60° | 1/2 |
| 90° | 0 |
Tangente
La tangente di un angolo si ottiene dividendo la lunghezza del cateto opposto per quella del cateto adiacente. Di seguito la formula generica:
- Tangente (α) = lunghezza del cateto opposto / lunghezza del cateto adiacente
La tabella mostra i valori di tangente per gli angoli precedentemente menzionati:
| Angolo (α) | Tangente (tan α) |
|---|---|
| 0° | 0 |
| 30° | √3/3 |
| 45° | 1 |
| 60° | √3 |
| 90° | Non definita |
Ogni funzione trigonometrica si applica agli angoli da 0 a 90 gradi in un triangolo rettangolo e ha un’importanza fondamentale nell’ambito della trigonometria.
Calcolo dell’ipotenusa
Il calcolo dell’ipotenusa di un triangolo rettangolo si basa sul Teorema di Pitagora. Il teorema stabilisce che in un triangolo rettangolo, l’ipotenusa, che è il lato opposto all’angolo retto, è uguale alla radice quadrata della somma dei quadrati degli altri due lati, noti come cateti.
Per calcolare l’ipotenusa c, si applica la seguente formula matematica:
![]()
dove:
- a è la lunghezza di uno dei cateti
- b è la lunghezza dell’altro cateto
Ecco una rappresentazione in formato tabellare:
| Simbolo | Descrizione | Formato matematico |
|---|---|---|
| a | Lunghezza del primo cateto | Lunghezza in unità |
| b | Lunghezza del secondo cateto | Lunghezza in unità |
| c | Lunghezza dell’ipotenusa |
Per eseguire il calcolo, si inseriscono i valori numerici di a e b nella formula e si esegue l’operazione di radice quadrata sulla somma dei loro quadrati. Questo processo fornisce la lunghezza esatta dell’ipotenusa.
La misura dell’ipotenusa può essere impiegata in diverse applicazioni pratiche come l’architettura, l’ingegneria o nel campo della navigazione, per citarne alcune. Esempi concreti di calcolo dell’ipotenusa includono la determinazione della distanza più breve tra due punti in uno spazio bidimensionale o la misurazione di elementi come scale, tetti e ponti.
Calcolo dei cateti
Per calcolare i cateti in un triangolo rettangolo, si utilizzano le funzioni trigonometriche note come seno e coseno. I cateti sono i due lati più corti che formano l’angolo retto. La relazione tra i lati e gli angoli in un triangolo rettangolo è determinata dal teorema di Pitagora.
Seno di un angolo (∠A) nel triangolo rettangolo è il rapporto tra il cateto opposto all’angolo e l’ipotenusa (i):![]()
Coseno di un angolo (∠A) è il rapporto tra il cateto adiacente all’angolo e l’ipotenusa:![]()
Per trovare la lunghezza dei cateti, si procede nel seguente modo:
- Identificare l’angolo noto e la lunghezza dell’ipotenusa o del cateto disponibile.
- Applicare la funzione trigonometrica appropriata per determinare la lunghezza del cateto desiderato.
| Angolo | Funzione | Formula |
|---|---|---|
| ∠A | Seno (per opposto) | opposto = i * sin(A) |
| ∠A | Coseno (per adiacente) | adiacente = i * cos(A) |
In assenza dell’ipotenusa, è possibile utilizzare il teorema di Pitagora:![]()
In questo modo, con la lunghezza di un cateto e dell’ipotenusa, si può risalire all’altro cateto.
Si ricorda che i risultati devono essere esatti o approssimati a seconda della precisione richiesta. Utilizzare strumenti di calcolo o tabelle trigonometriche per ottenere valori precisi.
Uso delle funzioni inverse
Le funzioni inverse trigonometriche permettono di determinare gli angoli di un triangolo rettangolo conoscendo le lunghezze dei lati. Sono essenziali per risolvere problemi di trigonometria nel triangolo rettangolo.
Arcoseno
L’arcoseno è la funzione inversa del seno e viene utilizzata per trovare l’angolo a partire dal rapporto tra il cateto opposto e l’ipotenusa. Si rappresenta con il simbolo asin o sin⁻¹. Ad esempio:
| Cateto Opposto | Ipotenusa | Angolo |
|---|---|---|
| 3 | 5 | asin(3/5) ≈ 36.87° |
Arcocoseno
L’arcocoseno, indicato come acos o cos⁻¹, è la funzione inversa del coseno. Serve a calcolare l’angolo avendo il rapporto tra il cateto adiacente e l’ipotenusa. Di seguito un esempio pratico:
| Cateto Adiacente | Ipotenusa | Angolo |
|---|---|---|
| 4 | 5 | acos(4/5) ≈ 36.87° |
Arcotangente
L’arcotangente, espressa come atan o tan⁻¹, è la funzione inversa della tangente. Consente di trovare l’angolo quando si conosce il rapporto tra il cateto opposto e il cateto adiacente. Esempio utilizzando l’arcotangente:
| Cateto Opposto | Cateto Adiacente | Angolo |
|---|---|---|
| 3 | 4 | atan(3/4) ≈ 36.87° |
Applicazioni pratiche della trigonometria
La trigonometria si presenta come strumento essenziale in molteplici campi pratici. Questa branca della matematica si occupa dello studio delle relazioni tra gli angoli e i lati dei triangoli, particolarmente focalizzata su quelli rettangoli, dove un angolo misura precisamente 90°.
In geodesia e topografia, la trigonometria permette di determinare la distanza tra due punti su superfici piane o sferiche, facilitando la creazione di mappe accurate e la misurazione di terreni. Utilizzando semplici formule trigonometriche, i topografi possono calcolare altezze e distanze inaccessibili direttamente.
Nel campo dell’ingegneria, la trigonometria è applicata nella progettazione di strutture e sistemi meccanici. Per esempio, nel calcolo delle forze agendo su componenti strutturali o nell’analisi del movimento di parti meccaniche, come nelle boccole di un motore.
L’astronomia fa affidamento sulla trigonometria per computare le distanze degli astri e la loro posizione in cielo. Tecniche come la parallasse sfruttano le funzioni trigonometriche per stimare la distanza di stelle e pianeti rispetto alla Terra.
Anche l’elettronica si avvale della trigonometria, in particolar modo per analizzare circuiti elettrici che utilizzano correnti alternate, dove le grandezze elettriche variano ciclicamente seguendo funzioni sinusoidali.
Di seguito, una tabella riassuntiva:
| Campo | Applicazione della trigonometria |
|---|---|
| Geodesia e Topografia | Misurazione di distanze e altezze |
| Ingegneria | Progettazione strutturale e analisi del movimento |
| Astronomia | Calcolo delle distanze e posizionamento di astri |
| Elettronica | Analisi di circuiti con correnti alternate |
Quest’utenza pratica evidenzia l’importanza fondamentale della trigonometria nelle attività quotidiane ed in contesti più complessi, rivelandosi indispensabile in diversi ambiti scientifici e tecnologici.
Il teorema di Pitagora
Il teorema di Pitagora afferma che, in un triangolo rettangolo, l’area del quadrato costruito sull’ipotenusa (il lato opposto all’angolo retto) è uguale alla somma delle aree dei quadrati costruiti sui due cateti (i lati che formano l’angolo retto). Tale teorema può essere matematicamente espresso come ![]() , dove:
, dove:
- ( a ) e ( b ) rappresentano la lunghezza dei cateti,
- ( c ) indica la lunghezza dell’ipotenusa.
Utilizzando questa relazione fondamentale, è possibile calcolare la lunghezza di un lato di un triangolo rettangolo conoscendo le lunghezze degli altri due. Il teorema prende il nome dal matematico greco Pitagora, benché la sua scoperta sia precedentemente documentata in altre culture.
La importanza di questo teorema nell’ambito trigonometrico si riflette anche nelle funzioni trigonometriche di seno, coseno e tangente, le quali possono essere definite attraverso le proporzioni tra i lati di un triangolo rettangolo.
Esempio pratico:
Per calcolare la lunghezza dell’ipotenusa ( c ), avendo i cateti di lunghezza 3 cm e 4 cm, applichiamo il teorema di Pitagora:
![]()
Quindi ![]() cm.
cm.
| Cateto 1 (a) | Cateto 2 (b) | Ipotenusa (c) |
|---|---|---|
| 3 | 4 | 5 |
L’applicazione del teorema di Pitagora è essenziale per la risoluzione di molteplici problemi pratici in ingegneria, fisica, architettura, e oltre.
La legge dei seni e dei coseni
Nell’ambito della trigonometria, la legge dei seni e la legge dei coseni sono relazioni fondamentali utilizzate per calcolare i diversi elementi di un triangolo. Entrambe le leggi sono applicabili nei triangoli rettangoli e quelli non rettangoli.
La legge dei seni stabilisce che il rapporto tra la lunghezza di un lato di un triangolo e il seno dell’angolo opposto è costante per tutti i lati e angoli del triangolo. La formula è la seguente:
![]()
Dove a, b, e c sono le lunghezze dei lati del triangolo, e α, β, e γ sono gli angoli opposti rispettivamente a questi lati.
La legge dei coseni, d’altro canto, è utile per trovare un lato di un triangolo quando si conoscono gli altri due e l’angolo tra di essi, o per determinare l’ampiezza di un angolo conoscendo tutti e tre i lati. La formula è:
![]()
Qui c è il lato del triangolo opposto all’angolo γ, mentre a e b sono i lati adiacenti all’angolo.
Queste leggi sono particolarmente preziose quando si studiano triangoli in cui non si applicano le formule base della trigonometria come il teorema di Pitagora, che è limitato ai soli triangoli rettangoli. In trigonometria, la legge dei seni e dei coseni permette l’analisi e il calcolo di triangoli di qualsiasi tipo.
Formule di angoli associati
In trigonometria, le formule di angoli associati sono utilizzate per esprimere le funzioni trigonometriche di angoli che si ottengono sommando o sottraendo un angolo noto, tipicamente di 30°, 45° o 60°, con un multiplo di 90°. Esse sono particolarmente rilevanti nel contesto dei triangoli rettangoli.
Per un angolo ( ![]() ), le relazioni fondamentali sono:
), le relazioni fondamentali sono:
Seno di ( 90° \pm θ ):
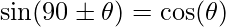
Coseno di ( 90° \pm θ ):
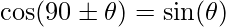
Tangente di ( 90° \pm θ ):
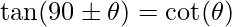
Le formule di angoli associati si applicano anche alle funzioni cotangente, secante e cosecante.
Ecco una rappresentazione tabulare di queste formule:
| Funzione | Formula per ( 90° + \theta ) | Formula per ( 90° – \theta ) |
|---|---|---|
| Seno | ||
| Coseno | ||
| Tangente | ||
| Cotangente | ||
| Secante | ||
| Cosecante |
L’uso di queste formule è cruciale nella semplificazione delle espressioni trigonometriche e nella risoluzione di problemi geometrici e trigonometrici complessi. La relazione tra seno e coseno attraverso l’angolo complementare è fondamentale nei triangoli rettangoli dove ogni angolo acuto è complementare all’altro.
Errori comuni e come evitarli
Quando si utilizza una calcolatrice trigonometrica per risolvere questioni riguardanti un triangolo rettangolo, è importante prestare attenzione ad alcuni errori ricorrenti. Per agevolare la comprensione e l’applicazione corretta dei concetti trigonometrici, di seguito sono elencati gli errori più comuni insieme a metodi per evitarli:
Errore nell’uso delle unità di misura: Assicurarsi che le unità di misura siano coerenti.
- Evitare: Utilizzo di gradi quando si dovrebbero usare i radianti o viceversa.
- Soluzione: Verificare sempre le impostazioni della calcolatrice prima di iniziare i calcoli.
Ambiguità nella scelta dell’angolo: Riconoscere correttamente gli angoli in un triangolo rettangolo.
- Evitare: Confusione tra angolo opposto e adiacente rispetto all’ipotenusa.
- Soluzione: Identificare chiaramente l’angolo di riferimento prima di applicare le funzioni trigonometriche.
Mancata comprensione delle formule:
- Evitare: Applicazione errata delle formule trigonometriche.
- Soluzione: Memorizzare le funzioni seno, coseno e tangente relative ai lati di un triangolo rettangolo:
- Seno (angolo) = cateto opposto / ipotenusa
- Coseno (angolo) = cateto adiacente / ipotenusa
- Tangente (angolo) = cateto opposto / cateto adiacente
Input errati nella calcolatrice:
- Evitare: Inserimento di numeri sbagliati o sequenze di operazioni errate.
- Soluzione: Raddoppiare la verifica dei dati inseriti e procedere passo dopo passo.
L’applicazione attenta di questi principi può migliorare notevolmente l’accuratezza dei risultati ottenuti utilizzando una calcolatrice trigonometrica nel contesto di un triangolo rettangolo.
Strumenti e software per la trigonometria
Con l’avvento della tecnologia informatica, è sorta una vasta gamma di strumenti e software per assistere negli studi e nelle applicazioni della trigonometria. Questi variano da semplici calcolatrici online a software più complessi per l’elaborazione grafica e l’analisi scientifica.
Calcolatrici Online:
- GeoGebra: un software interattivo che permette la manipolazione di figure geometriche e offre funzionalità per il calcolo di funzioni trigonometriche.
- Desmos: una piattaforma grafica che consente agli utenti di visualizzare e esplorare funzioni matematiche, inclusi grafici trigonometrici.
Applicazioni Mobili:
- MyScript Calculator: quest’app trasforma la scrittura manuale in input digitali, permettendo agli utenti di eseguire calcoli trigonometrici in modo intuitivo.
- Mathway: un’app che funge da tutor digitale e offre un vasto supporto sui problemi di trigonometria, generando passaggi di risoluzione e risposte.
Software Professionali:
- MATLAB: una piattaforma di alto livello e un ambiente per il calcolo numerico e la visualizzazione che comprende strumenti per l’analisi trigonometrica.
- Maple: una suite software che fornisce strumenti per l’analisi matematica, inclusa la trigonometria, con un forte enfoque sulla risoluzione simbolica e numerica.
Ecco una tabella che riassume alcune delle caratteristiche principali di queste risorse:
| Strumento | Piattaforma | Caratteristiche principali |
|---|---|---|
| GeoGebra | Online/Desktop | Manipolazione grafica, calcolo interattivo |
| Desmos | Online/App | Visualizzazione funzioni, grafici interattivi |
| MyScript Calculator | App | Input scrittura manuale, calcoli immediati |
| Mathway | Online/App | Tutoraggio digitale, step di risoluzione |
| MATLAB | Desktop | Calcolo numerico avanzato, visualizzazione, analisi trigonometrica |
| Maple | Desktop | Risoluzione simbolica e numerica, analisi matematica |
Questi sono solo alcuni degli strumenti a disposizione degli studenti e dei professionisti che lavorano con la trigonometria. Ogni strumento ha le proprie specificità e può essere scelto in base alle esigenze individuali.