Il volume di un cono è la quantità di spazio tridimensionale che esso occupa. Per calcolarlo, si utilizza la formula matematica:
![]()
Dove:
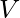 rappresenta il volume,
rappresenta il volume,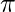 è una costante matematica, approssimata a 3,14159,
è una costante matematica, approssimata a 3,14159,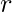 è il raggio della base del cono,
è il raggio della base del cono,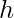 è l’altezza del cono, misurata come la distanza verticale dall’apice alla base.
è l’altezza del cono, misurata come la distanza verticale dall’apice alla base.
Il fattore ![]() indica che il volume del cono è un terzo di quello di un cilindro avente stessa base e altezza. Il calcolo si fonda sul principio di Cavalieri, per il quale solidi di altezza uguale e che mantengono un’area di sezione trasversale costante in una direzione, hanno uguali volumi.
indica che il volume del cono è un terzo di quello di un cilindro avente stessa base e altezza. Il calcolo si fonda sul principio di Cavalieri, per il quale solidi di altezza uguale e che mantengono un’area di sezione trasversale costante in una direzione, hanno uguali volumi.
A titolo di esemplificazione, si presenta una tabella con i valori di volume per coni di diverse dimensioni (considerando ![]() come 3.14):
come 3.14):
| Raggio (r) | Altezza (h) | Volume (V) |
|---|---|---|
| 1 cm | 1 cm | 1.05 cm³ |
| 2 cm | 3 cm | 12.57 cm³ |
| 5 cm | 10 cm | 261.80 cm³ |
Il calcolo del volume di un cono è rilevante in vari campi come la geometria, l’ingegneria, l’architettura e in diverse applicazioni pratiche, inclusa la produzione di oggetti conici o nel settore dell’edilizia.
Calcolatore volume del cono
Matematica per il calcolo del volume
Il volume di un cono si calcola utilizzando la formula matematica ![]() , dove
, dove ![]() rappresenta il volume,
rappresenta il volume, ![]() il raggio della base e
il raggio della base e ![]() l’altezza del cono. La costante
l’altezza del cono. La costante ![]() , approssimativamente pari a 3.14159, è fondamentale per il calcolo di aree e volumi nell’ambito delle figure circolari.
, approssimativamente pari a 3.14159, è fondamentale per il calcolo di aree e volumi nell’ambito delle figure circolari.
Per determinare il volume di un cono, è necessario seguire questi passaggi:
- Misurare il raggio
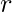 della base.
della base. - Misurare l’altezza
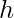 del cono dalla punta alla base.
del cono dalla punta alla base. - Elevar al quadrato il raggio
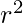 .
. - Moltiplicare
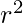 per
per 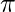 .
. - Moltiplicare il risultato per
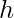 .
. - Dividere il prodotto finale per 3.
La formula è un’applicazione del principio di Cavalieri, che afferma che volumi di solidi di altezza uguale e sezioni trasversali che presentano la stessa area a ogni altezza, sono equivalenti tra loro.
Per un’applicazione pratica, si consideri un cono con un raggio di base di 4 cm e un’altezza di 9 cm. Seguendo i passaggi illustrati, il calcolo del suo volume sarà:
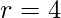 cm
cm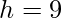 cm
cm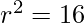 cm²
cm²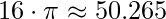 cm²
cm²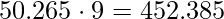 cm³
cm³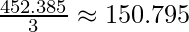 cm³
cm³
Pertanto, il volume del cono sarà approssimativamente 150.795 cm³.
Utilizzare strumenti adeguati di misurazione e calcolo è cruciale per ottenere risultati precisi. La presenza di ![]() nella formula implica che il raggio influenzi maggiormente il volume rispetto all’altezza, dato che compare con esponente quadrato.
nella formula implica che il raggio influenzi maggiormente il volume rispetto all’altezza, dato che compare con esponente quadrato.
Formula per il volume del cono
Per calcolare il volume di un cono, si utilizza una formula matematica specifica che dipende dalle misure del cono stesso. Il volume rappresenta lo spazio tridimensionale occupato dal cono.
Volume con raggio e altezza
La formula per determinare il volume di un cono quando sono noti il raggio (r) della base e l’altezza (h) è:
V = (1/3)πr²h
Dove:
- V è il volume del cono
- π è una costante matematica (circa 3.14159)
- r è il raggio della base del cono
- h è l’altezza del cono dalla base al vertice
Per esempio, se il raggio della base è di 3 cm e l’altezza è di 4 cm, il volume del cono è calcolato come segue:
V = (1/3)π(3 cm)²(4 cm) ≈ 37.68 cm³
Volume con diametro e altezza
Nel caso in cui siano noti il diametro (d) della base e l’altezza (h), si può prima calcolare il raggio (r = d/2), e poi utilizzare la formula del volume come segue:
V = (1/3)π(d/2)²h
Dove:
- V è il volume del cono
- d è il diametro della base del cono
- h è l’altezza del cono
Se il diametro della base è di 6 cm e l’altezza è di 4 cm, il volume si calcola dividendo dapprima il diametro per due per trovare il raggio, e poi applicando la formula del volume:
r = d/2 = 6 cm / 2 = 3 cm
V = (1/3)π(3 cm)²(4 cm) ≈ 37.68 cm³
Applicazioni pratiche del calcolo del volume
Il calcolo del volume di un cono trova utilizzo in svariati ambiti. In geometria e ingegneria, serve per progettare oggetti con questa forma specifica e per calcolare la capacità di contenimento. Nel settore edile, si utilizza per stabilire la quantità di materiali necessari per costruzioni con forme coniche, come tetti o cupole.
In matematica applicata, il volume del cono è essenziale per risolvere problemi di ottimizzazione, ad esempio, quando si vuole massimizzare il volume di contenitori conici con limitazioni sulle dimensioni. In industria alimentare, specialmente nella produzione di coni gelato, questo calcolo è cruciale per standardizzare le dimensioni e massimizzare l’efficienza di riempimento.
Segue una tabella che mostra le formule per il calcolo del volume in base a vari parametri:
| Parametro | Formula del volume | Descrizione |
|---|---|---|
| Raggio (r) e altezza (h) | La base del cono è un cerchio con raggio | |
| Diametro (d) e altezza (h) | Il diametro |
L’analisi di impatto ambientale si avvale del calcolo del volume per stimare la capacità di contenitori conici utilizzati per raccogliere rifiuti speciali o sostanze pericolose. In farmacologia, il calcolo del volume di un cono può essere essenziale per la progettazione di strumenti come imbuto, che facilitano la manipolazione di polveri o liquidi.
Il settore dell’intrattenimento, in particolare la progettazione di giochi o scenografie, impiega tali calcoli per strutturare oggetti scenici e garantire proporzioni corrette. In sintesi, la conoscenza e l’applicazione del calcolo del volume del cono si rivelano essere strumenti decisivi in molti settori produttivi e scientifici.
Strumenti di calcolo online
Gli strumenti di calcolo online forniscono agli utenti la possibilità di calcolare il volume di un cono in modo semplice e rapido. Questi strumenti richiedono in genere l’inserimento di alcuni parametri di base come il raggio della base ![]() e l’altezza
e l’altezza ![]() .
.
Parametri richiesti:
- Raggio (r): Distanza dal centro della base alla sua periferia.
- Altezza (h): Distanza dalla base alla punta del cono.
Questi calcolatori utilizzano la formula del volume del cono ![]() , dove
, dove ![]() è il rapporto costante tra la circonferenza di un cerchio e il suo diametro, approssimativamente 3.14159.
è il rapporto costante tra la circonferenza di un cerchio e il suo diametro, approssimativamente 3.14159.
Tabella dei calcolatori più comuni:
| Calcolatore | Input necessari | Lingua dell’interfaccia | Caratteristiche aggiuntive |
|---|---|---|---|
| GeometriaOnline | Raggio, Altezza | Italiano | Visualizzazione 3D |
| CalcioCono | Diametro, Altezza | Multilingua | Conversione unità di misura |
| MatematicaVirtuale | Raggio, Altezza, Angolo | Italiano | Grafico del cono |
Istruzioni per l’uso sono fornite per aiutare l’utente a inserire correttamente i dati. Dopo aver imputato i parametri, il risultato viene subito elaborato e presentato all’utente.
L’accessibilità da diversi dispositivi, come computer, tablet e smartphone, è assicurata, consentendo agli utenti di effettuare calcoli in movimento. La precisione dei risultati dipende dall’accuratezza dei dati inseriti. L’utilizzo di questi calcolatori è utile in ambito educativo e professionale per risolvere problemi di geometria e ingegneria.
Esempi di calcolo del volume del cono
Per calcolare il volume di un cono si utilizza la formula:
![]()
dove ![]() è il volume,
è il volume, ![]() è il raggio della base e
è il raggio della base e ![]() è l’altezza del cono.
è l’altezza del cono.
Esempio 1:
Consideriamo un cono con un raggio di base ![]() cm e un’altezza
cm e un’altezza ![]() cm. Il volume sarà calcolato come segue:
cm. Il volume sarà calcolato come segue:![]()
![]()
Di conseguenza, il volume del cono è ![]() centimetri cubi.
centimetri cubi.
Esempio 2:
Per un cono di raggio ![]() cm e altezza
cm e altezza ![]() cm, il volume si calcola così:
cm, il volume si calcola così:![]()
![]()
![]()
Il volume ottenuto è ![]() centimetri cubi.
centimetri cubi.
Di seguito, una tabella che schematizza i dati degli esempi:
| Esempio | Raggio (cm) | Altezza (cm) | Volume (cm^3) |
|---|---|---|---|
| Esempio 1 | 3 | 4 | |
| Esempio 2 | 5 | 10 |
Questi esempi illustrano come applicare la formula per calcolare il volume di un cono in situazioni specifiche.
Calcolo di volumi per coni tronchi
Il calcolo di volumi per coni tronchi è una procedura matematica che richiede l’applicazione di formule specifiche.
Definizione di cono tronco
Un cono tronco si ottiene dalla sezione di un cono per mezzo di un piano parallelo alla base. Questa figura geometrica è caratterizzata da due basi circolari a raggio differente.
Formula per il volume del cono tronco
Per calcolare il volume di un cono tronco si utilizza la seguente formula:
Volume (V) = (1/3) * π * h * (R^2 + R * r + r^2)
dove h rappresenta l’altezza del cono tronco, R il raggio della base maggiore e r il raggio della base minore.
Errori comuni nel calcolo del volume
Nel calcolo del volume di un cono, sono frequenti alcuni errori che possono portare a stime inaccurate. Di seguito, alcuni degli equivoci più comuni:
Misurazione imprecisa: Il volume di un cono si calcola con la formula
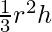 , dove
, dove 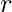 è il raggio della base e
è il raggio della base e 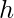 è l’altezza. Una misurazione imprecisa del raggio o dell’altezza può portare a un risultato errato.
è l’altezza. Una misurazione imprecisa del raggio o dell’altezza può portare a un risultato errato.Utilizzo di unità diverse: Se il raggio è misurato in centimetri e l’altezza in metri, il calcolo sarà errato a meno che non si convertano entrambe le misure nella stessa unità.
Trascurare il fattore
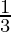 : Dimenticare di moltiplicare per
: Dimenticare di moltiplicare per 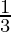 è un errore frequente che triplica erroneamente il volume del cono.
è un errore frequente che triplica erroneamente il volume del cono.Confusione tra diametro e raggio: È importante distinguere tra diametro, che è la distanza attraverso il centro del cerchio dalla base del cono, e raggio, che è metà del diametro. Usare il diametro al posto del raggio nel calcolo quadruplica il valore del volume.
Per evitare errori:
- Verificare le misurazioni: Assicurarsi che il raggio e l’altezza siano accurati e omogenei.
- Controllare le unità di misura: Convertire tutte le unità in un sistema coerente prima di calcolare.
- Rivedere la formula: Assicurarsi di applicare correttamente la formula, includendo il fattore
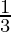 .
. - Distinguere raggio e diametro: Assicurarsi di usare il raggio nella formula del volume e non il diametro.
Evitando questi errori comuni, si assicura un calcolo del volume più preciso e affidabile di un cono.
Consigli per la misurazione accurata
Per misurare il volume di un cono, è fondamentale utilizzare strumenti di misurazione precisi. Il volume ![]() di un cono si calcola con la formula
di un cono si calcola con la formula ![]() , dove
, dove ![]() rappresenta il raggio della base e
rappresenta il raggio della base e ![]() l’altezza del cono. Qui sono elencati alcuni consigli per assicurare che le misurazioni siano quanto più accurate possibile.
l’altezza del cono. Qui sono elencati alcuni consigli per assicurare che le misurazioni siano quanto più accurate possibile.
Utilizzo del Calibro Vernier: Per misurare il diametro della base, si consiglia l’uso del calibro Vernier, che permette una lettura precisa fino a 0,02 mm. Il raggio sarà la metà del diametro misurato.
Misurazione dell’Altezza con Rigorosità: L’altezza deve essere misurata dalla punta del cono fino alla base, lungo l’asse centrale. Un righello o un metro a nastro può servire allo scopo, assicurandosi che sia perfettamente perpendicolare alla base per la lettura.
| Strumento | Utilizzo |
|---|---|
| Calibro Vernier | Misura del diametro della base |
| Righello o Metro a nastro | Misura dell’altezza del cono |
Verifica della Perpendicularità: Durante la misura dell’altezza, verificare che lo strumento di misurazione sia perpendicolare alla superficie di base per evitare distorsioni.
Correzione Ambientale: Tenere conto delle condizioni ambientali che potrebbero influenzare le misurazioni, come la temperatura e l’umidità, che potrebbero causare espansione o contrazione dei materiali.
Ripetizione delle Misure: Effettuare più misurazioni per ogni dimensione e calcolare la media per ridurre l’errore casuale.
Utilizzando queste pratiche si possono ridurre significativamente gli errori di misurazione e calcolare un volume che rifletta più fedelmente le dimensioni reali del cono.
Integrazione del calcolo del volume in software
Il calcolo del volume di un cono è un’applicazione matematica comunemente integrata nei software CAD (Computer-Aided Design) e in altri strumenti di modellazione 3D. Questa funzione permette agli utenti di determinare facilmente il volume di coni all’interno di progetti complessi.
Formula di Calcolo:
Il volume ![]() di un cono si calcola con la formula:
di un cono si calcola con la formula:
![]()
dove ![]() è il raggio della base e
è il raggio della base e ![]() è l’altezza del cono.
è l’altezza del cono.
Implementazione nei Software:
- Input dell’Utente:
- Utenti inseriscono i valori di raggio
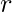 e altezza
e altezza 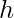 .
.
- Utenti inseriscono i valori di raggio
- Metodo di Calcolo:
- Il software esegue automaticamente l’operazione matematica.
- Output Grafico:
- Rappresentazione visuale del cono con indicazione del volume.
Vantaggi dell’Integrazione:
- Efficienza:
- Il calcolo è immediato e riduce errori manuali.
- Precisione:
- Risultati accurati utili per progettazione e produzione.
- Interoperabilità:
- Compatibile con vari formati e piattaforme di scambio dati.
L’integrazione di questa funzione è cruciale per il settore dell’ingegneria e dell’architettura, facilitando la progettazione di componenti e la gestione di materiali. I software aggiornati includono solitamente questa caratteristica per migliorare l’efficacia del processo di progettazione.
Impatto dell’errore di calcolo sul volume totale
In geometria, il cono è una figura solida che si estende da una base circolare fino a un punto, chiamato vertice o apice. Il volume del cono (V) si calcola utilizzando la formula: ![]() , dove
, dove ![]() rappresenta il raggio della base e
rappresenta il raggio della base e ![]() l’altezza del cono.
l’altezza del cono.
Un errore nel calcolo di uno qualsiasi di questi parametri può portare a una stima imprecisa del volume totale. Le cause possono variare dall’errore di misurazione a un’imprecisione durante l’inserimento dei dati.
| Errore | Impatto sul Volume |
|---|---|
| Raggio (r) | Incremento o decremento proporzionale al quadrato di r. |
| Altezza (h) | Incremento o decremento lineare con h. |
Ad esempio, un errore del 5% nella misurazione dell’altezza influenzerà il volume totale del cono molto meno rispetto allo stesso errore percentuale nella misurazione del raggio, a causa della potenza al quadrato del raggio nella formula.
L’errore relativo del volume può essere espresso come somma degli errori relativi dei termini nella formula, ovvero:
- Errore relativo su r: Se
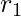 è il raggio misurato e
è il raggio misurato e 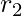 è il raggio reale,
è il raggio reale, 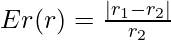
- Errore relativo su h: Se
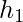 è l’altezza misurata e
è l’altezza misurata e 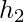 è l’altezza reale,
è l’altezza reale, 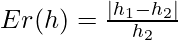
Dunque, è fondamentale approcciarsi al calcolo con attenzione, dato che un piccolo errore può avere un significativo impatto sul risultato finale.
Domande frequenti sul calcolo del volume del cono
Q: Qual è la formula per calcolare il volume di un cono?
A: Il volume ![]() di un cono si calcola utilizzando la formula:
di un cono si calcola utilizzando la formula:![]()
dove ![]() è il raggio della base e
è il raggio della base e ![]() è l’altezza del cono.
è l’altezza del cono.
Q: È possibile calcolare il volume di un cono con base ellittica?
A: Sì, per un cono con base ellittica si utilizza una formula leggermente diversa:![]()
con ![]() e
e ![]() che rappresentano i semiassi dell’ellisse che forma la base e
che rappresentano i semiassi dell’ellisse che forma la base e ![]() l’altezza del cono.
l’altezza del cono.
Q: Come si misura l’altezza del cono per il calcolo del volume?
A: L’altezza ![]() di un cono è la distanza perpendicolare dal vertice alla base. È importante che la misurazione sia perpendicolare alla base per un calcolo accurato.
di un cono è la distanza perpendicolare dal vertice alla base. È importante che la misurazione sia perpendicolare alla base per un calcolo accurato.
Q: Che unità di misura si devono utilizzare nel calcolo del volume?
A: Le unità di misura per il raggio e l’altezza devono essere coerenti. Se si misurano in centimetri, il volume sarà espresso in centimetri cubi (cm³). La corrispondenza delle unità di misura è essenziale per un risultato esatto.
Q: Cosa succede al volume del cono se si raddoppia l’altezza?
A: Se si raddoppia l’altezza ![]() , il volume del cono aumenterà di due volte, in quanto l’altezza appare linearmente nella formula del volume.
, il volume del cono aumenterà di due volte, in quanto l’altezza appare linearmente nella formula del volume.
Q: In quale contesto potrebbe essere necessario calcolare il volume del cono?
A: Il calcolo del volume può essere necessario in varie situazioni, come nel design industriale, nell’architettura, nella creazione di imballaggi, o in ambito educativo per lo studio della geometria spaziale.